|
|
|
|
|
§ 3. Умножение и деление натуральных чисел 15. Порядок выполнения действий
Сложение и вычитание чисел называют действиями первой ступени, а умножение и деление чисел — действиями второй ступени.
Порядок выполнения действий при нахождении значений выражений определяется следующими правилами:
1. Если в выражении нет скобок и оно содержит действия только одной ступени, то их выполняют по порядку слева направо. 2. Если выражение содержит действия первой и второй ступени и в нём ; нет скобок, то сначала выполняют действия второй ступени, потом — действия первой ступени. 3. Если в выражении есть скобки, то сначала выполняют действия в скобках (учитывая при этом правила 1 и 2).
Пример 1. Найдём значение выражения 800 - 625 + 331 + 87 - 119. Это выражение не имеет скобок и содержит действия только первой ступени, поэтому следует выполнять действия по порядку слева направо: 800 - 625 = 175, 175 + 331 = 506, 506 + 87 = 593, 593 - 119 = 474. Итак, значение выражения равно 474. Пример 2. Найдём значение выражения 780 : 39 • 212 : 106 • 13. Это выражение не содержит скобок, и в нём имеются действия только второй ступени, поэтому их следует выполнять по порядку слева направо: 780 : 39 = 20, 20 • 212 = 4240, 4240 : 106 = 40, 40 • 13 = 520. Итак, значение выражения равно 520. Пример 3. Найдём значение выражения 5781 - 28 • 75 : 25 + 156 : 12. Это выражение не содержит скобок, и в нём есть действия первой и второй ступени. Поэтому вначале выполним действия второй ступени: 28 • 75 = = 2100, 2100 : 25 = 84, 156 : 12 = 13, а потом действия первой ступени: 5781 - 84 = 5697, 5697 + 13 = 5710. Значение выражения равно 5710. Пример 4. Найдём значение выражения 36000 : (62 + 14 • 2) - 23 • 5. Это выражение содержит скобки. Поэтому выполним сначала действия в скобках: 62 + 14 • 2 = 62 + 28 = 90. Подставив это значение, получим: 36 000 : 90 - 23 • 5. Вычислив значение последнего выражения, получим 285.
В выражениях, содержащих скобки, можно эти скобки не писать, если при этом порядок действий не изменяется.
Пример 5. Вместо (53 - 12) + 14 можно написать 53 - 12 + 14, так как в обоих случаях порядок действий одинаков: 53 - 12 = 41, 41 + 14 = 55.
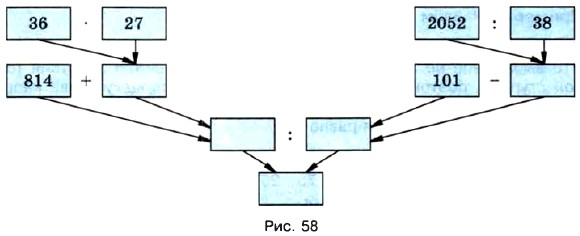
Изменять порядок действий можно на основе свойств сложения, вычитания и умножения. Каждое выражение задаёт программу своего вычисления. Она состоит из команд. Например, программа вычисления выражения (814 + 36 • 27) : (101 - 2052 : 38) состоит из следующих команд: 1. Перемножить числа 36 и 27.
Эту программу вычислений можно изобразить в виде схемы (рис. 58). Последовательно выполнив действия и заполнив при этом пустые клетки, получим в нижней клетке ответ.
|
|
|