|
|
|
|
|
Глава 2. Постоянный электрический ток Закон Ома для участка цепи. Сопротивление проводникаЕдиницы сопротивленияВ абсолютной системе единиц за единицу сопротивления принимают сопротивление проводника, в котором при напряжении на его концах в одну электростатическую единицу напряжения сила тока равна одной электростатической единице силы тока:
Единицей сопротивления в СИ является о м. 1 Ом — сопротивление проводника, в котором при напряжении на его концах в 1 В сила тока в нем равна 1 А.
Заметим, что термин «сопротивление» употребляют в двух смыслах: во-первых, электрическое сопротивление — это величина, определяющая силу тока при заданном напряжении. В этом смысле, например, говорят: лампа накаливания обладает сопротивлением 400 Ом или провод имеет сопротивление 0,5 Ом; во-вторых, резистором (или сопротивлением) называют устройство, предназначенное для включения в электрическую цепь с целью регулирования, уменьшения или ограничения тока цепи. Таким устройством может служить, например, реостат для регулирования силы тока в цепи путем изменения сопротивления. Резисторы широко применяются в радиоприемниках, телевизорах и других устройствах. Условное обозначение резистора показано на рисунке 2.12. Удельное сопротивлениеСопротивление зависит от материала проводника и его геометрических размеров. Опыт показывает, что при неизменной температуре сопротивление однородного проводника постоянного оечения прямо пропорционально его длине l и обратно пропорционально площади S поперечного сечения проводника:
Введем коэффициент пропорциональности и запишем последнюю зависимость в виде равенства
Коэффициент пропорциональности ρ численно равен сопротивлению проводника единичной длины и единичного поперечного сечения и называется удельным сопротивлением проводника. Удельное сопротивление зависит от рода вещества и его состояния (в первую очередь, от температуры). Из формулы (2.4.6) находим:
Отсюда видно, что единицей удельного сопротивления в СИ является
Ом-метр равен удельному сопротивлению проводника площадью поперечного сечения 1 м2 и длиной 1 м, имеющего сопротивление 1 Ом. Удельное сопротивление металлов мало. Например, удельное сопротивление обычной технической меди при 20 °С равно 1,72 • 10-8 Ом • м. Механическая и термическая обработка заметно влияет на электрическое сопротивление металлов. Так, после холодной протяжки удельное сопротивление медной проволоки возрастает до 1,77 • 10-8 Ом • м. Еще поразительнее зависимость сопротивления от наличия ничтожных примесей. Тщательная очистка уменьшает удельное сопротивление меди при температуре 20 °С до 1,69 • 10-8 Ом • м. Но достаточно добавить к меди 1% марганца, чтобы удельное сопротивление ее возросло до 4,8 • 10-8 Ом • м, т. е. почти в 3 раза! Примерно так же влияют на удельное сопротивление добавки железа, кобальта, иридия и др. У сплавов, содержащих примеси в значительном количестве, сопротивление очень велико. Удельное сопротивление этих сплавов в несколько раз больше, чем у каждой из составных частей. Так, Константин, состоящий из 60% меди и 40% никеля, имеет удельное сопротивление 4,4 • 10-7 Ом • м, в то время как у чистой меди оно равно 1,7 • 10-8 Ом • м, а у никеля — 7,2 • 10-8 Ом • м*. * Все данные здесь приведены для температуры 20 °С. «Королем» подобных сплавов можно назвать нихром, удельное сопротивление которого около 10-6 Ом • м. Недаром он нашел такое широкое применение в нагревательных приборах. Диэлектрики обладают очень большим, но конечным удельным сопротивлением. Так, удельное сопротивление фарфора 1013 Ом • м. В таблице 3 приведены примеры значений удельного сопротивления некоторых веществ. Величина, обратная удельному сопротивлению проводника, называется удельной проводимостью и обозначается буквой γ:
Единица удельной проводимости — (Ом • м)-1 Через удельную проводимость сопротивление проводника выражается так:
Закон Ома в дифференциальной форме
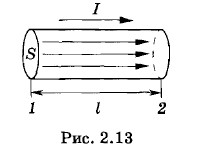
Закон Ома в форме (2.4.3) связывает силу тока в проводнике с напряжением на его концах и сопротивлением проводника. Используя ее, можно найти связь между плотностью тока Рассмотрим цилиндрический проводник длиной l и площадью поперечного сечения S (рис. 2.13). В нем устанавливается однородное стационарное поле с линиями напряженности, параллельными оси проводника (см. § 2.3). Поэтому разность потенциалов на концах проводника связана с напряженностью поля соотношением: φ1 - φ2 = El. (2.4.8) Силу тока при равномерном распределении плотности тока можно представить так: I = jS. (2.4.9) Подставив выражения (2.4.7), (2.4.8) и (2.4.9) в закон Ома (2.4.3), получим: j = γE. Вектор плотности тока
Это и есть закон Ома в дифференциальнойДлокальной) форме, так как связывает три величины — Мы получили закон Ома в форме (2.4.10) для частного случая однородного цилиндрического проводника. В действительности же он справедлив для проводников любой формы, как однородных, так и неоднородных.
|
|
|



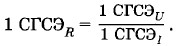
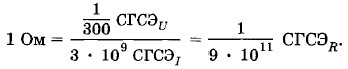


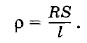
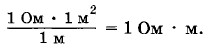
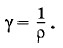


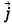 , удельной проводимостью γ и напряженностью поля
, удельной проводимостью γ и напряженностью поля 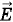 .
.

 надо хорошо осознать и запомнить.
надо хорошо осознать и запомнить.