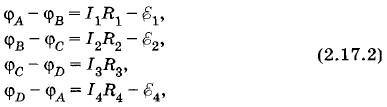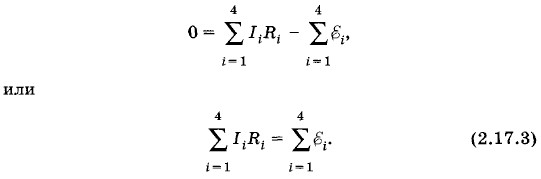|
|
|
|
|
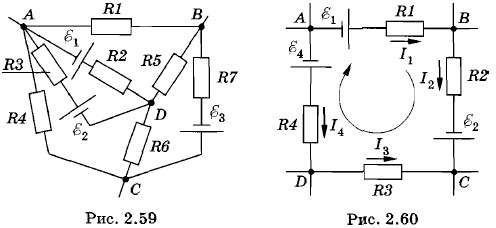
Глава 2. Постоянный электрический ток § 2.17. Расчет сложных электрических цепейВ общем случае электрическая цепь может быть образована несколькими источниками тока и резисторами, соединенными произвольным образом, например так, как показано на рисунке 2.59. Такая цепь называется сложной разветвленной электрической цепью. Сложную электрическую цепь можно разбить на ряд отдельных замкнутых контуров (см. рис. 2.59): ABDA, АВСА и т. д. Расчет таких цепей (например, нахождение сил токов во всех участках цепи) можно выполнить с помощью закона Ома. Однако во многих случаях расчет упрощается, если применить правила Кирхгофа. С первым правилом Кирхгофа (2.8.2) мы познакомились в § 2.8. Оно гласит: алгебраическая сумма сил токов в проводниках, сходящихся в узел, равна нулю. Теперь рассмотрим второе правило. Второе правило КирхгофаРассмотрим произвольно выбранный замкнутый контур ABCD (рис. 2.60). Применим к отдельным участкам этого контура закон Ома для участка цепи, содержащего источник ЭДС, в форме (2.15.3): φ1 - φ2 =Ir - Обозначим потенциалы узлов А, В, С и D соответственно через φА, φB, φC и φD. За направление обхода контура выберем направление по часовой стрелке. Тогда, согласно (2.17.1), можем написать:
где I1, I2, I3, I4 — силы токов,
Это и есть второе правило Кирхгофа: алгебраическая сумма падений напряжения в ветвях замкнутого контура равна алгебраической сумме ЭДС, действующих в этом контуре. В более общем виде второе правило Кирхгофа можно записать так:
|
|
|



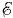 (2.17.1)
(2.17.1)