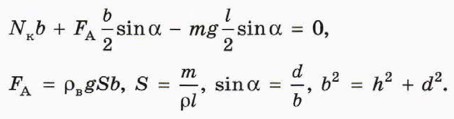|
§ 37. Гидростатика



Закон Архимеда (окончание)
 7. Ко дну аквариума прикреплена пружина, к верхнему концу которой прикреплён деревянный шар (рис. 37.4). Чему равна плотность дерева, если энергия упругой деформации пружины не изменилась после того, как в аквариум налили воду? Считайте, что шар полностью погружён в воду. 7. Ко дну аквариума прикреплена пружина, к верхнему концу которой прикреплён деревянный шар (рис. 37.4). Чему равна плотность дерева, если энергия упругой деформации пружины не изменилась после того, как в аквариум налили воду? Считайте, что шар полностью погружён в воду.
 8. Подвешенная за один конец тонкая пластмассовая палочка массой m и длиной l частично погружена в воду и находится в равновесии в наклонном положении (рис. 37.5). При этом длина погружённой в воду части палочки равна l1 Обозначим площадь поперечного сечения палочки S, плотность пластмассы ρп, плотность воды ρв. 8. Подвешенная за один конец тонкая пластмассовая палочка массой m и длиной l частично погружена в воду и находится в равновесии в наклонном положении (рис. 37.5). При этом длина погружённой в воду части палочки равна l1 Обозначим площадь поперечного сечения палочки S, плотность пластмассы ρп, плотность воды ρв.

а) Изобразите на чертеже действующие на палочку силу тяжести и силу Архимеда. Объясните, почему справедливы уравнения:
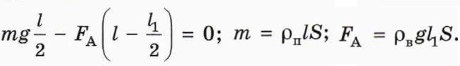
б) Чему равна плотность пластмассы, если l1 = 0,5l?
Палочка в стакане с водой
Вернёмся к палочке в стакане, рассмотренной в § 36. Но пусть теперь стакан доверху наполнен водой (рис. 37.6). Будем считать, что при этом положение палочки не изменилось.
 9. Как и почему изменилась сила давления края стакана на палочку после заполнения стакана водой? 9. Как и почему изменилась сила давления края стакана на палочку после заполнения стакана водой?
Введём обозначения:
l — длина палочки,
S — площадь её поперечного сечения,
m — масса палочки,
ρ — плотность палочки,
ρв — плотность воды,
h — высота стакана,
d — его диаметр.
Для упрощения формул удобно обозначить α угол между палочкой и вертикалью, а длину находящейся в стакане части палочки b (α и b можно выразить через h и d, но удобнее ввести для них свои обозначения, чтобы упростить формулы).
Силу, действующую на палочку со стороны края стакана, обозначим 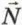 K, а силу Архимеда — K, а силу Архимеда — 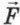 А. А.
 10. Обозначьте на чертеже в тетради все действующие на палочку силы и объясните, почему справедливы уравнения: 10. Обозначьте на чертеже в тетради все действующие на палочку силы и объясните, почему справедливы уравнения:
 11. В гладком цилиндрическом стакане диаметром 6 см и высотой 8 см находится тонкая палочка длиной 15 см. Плотность палочки в 2 раза больше плотности воды. Во сколько раз уменьшится сила давления палочки на край стакана после того, как его наполнят водой? 11. В гладком цилиндрическом стакане диаметром 6 см и высотой 8 см находится тонкая палочка длиной 15 см. Плотность палочки в 2 раза больше плотности воды. Во сколько раз уменьшится сила давления палочки на край стакана после того, как его наполнят водой?
<<< К началу
| 


 7. Ко дну аквариума прикреплена пружина, к верхнему концу которой прикреплён деревянный шар (рис. 37.4). Чему равна плотность дерева, если энергия упругой деформации пружины не изменилась после того, как в аквариум налили воду? Считайте, что шар полностью погружён в воду.
7. Ко дну аквариума прикреплена пружина, к верхнему концу которой прикреплён деревянный шар (рис. 37.4). Чему равна плотность дерева, если энергия упругой деформации пружины не изменилась после того, как в аквариум налили воду? Считайте, что шар полностью погружён в воду.


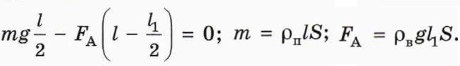

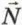 K, а силу Архимеда —
K, а силу Архимеда — 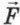 А.
А.