|
|
|
|
|
|
§ 37. Гидростатика Плавание телУсловие плавания телКогда тело плавает, действующая на него сила Архимеда
Это справедливо для любого тела и любой жидкости, причём независимо от того, погружено тело в жидкость полностью (рис. 37.7, а) или частично1 (рис. 37.7, б). 1 Точка приложения силы Архимеда может не совпадать с точкой приложения силы тяжести. Но поскольку здесь используется только первое условие равновесия, мы изображаем на чертеже эти силы приложенными в одной точке.
Плавание однородных телМасса m однородного тела связана с его плотностью ρТ и объёмом V соотношением m = ρТV. (5) А сила Архимеда равна весу жидкости в объёме погружённой части тела. Обозначим плотность жидкости ρж, а объём погружённой в жидкость части тела Vnoгp. Тогда FA = ρжgVnoгp. (6)
П о д с к а з к а. Воспользуйтесь формулами (4), (5), (6).
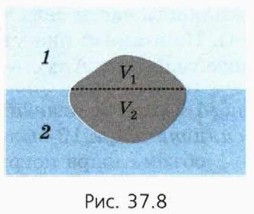
а) Для какого шарика объём погружённой части больше? б) Насколько объём погружённой части одного шарика больше, чем другого? Пусть теперь тело плавает на границе двух жидкостей (рис. 37.8). Как найти объём погружённой в каждую жидкость части тела?
Рассуждая как и при выводе выражения (3) для силы Архимеда, заменим части тела, находящиеся в разных жидкостях, двумя «телами» того же объёма и формы, состоящими из соответствующих жидкостей2. 2 При этом надо считать погружённой в верхнюю жидкость часть тела, находящуюся выше границы раздела жидкостей (пунктир на рисунке 37.10), а в нижнюю — ниже этой границы. Эти тела будут находиться в равновесии в «своих» жидкостях. Следовательно, равнодействующая сил давления, приложенных ко всем частям поверхности тела, направлена вверх и равна по модулю суммарному весу жидкостей в объёме, вытесненном телом.
ρ1V1 + ρ2V2 = ρтV.
|
|
|



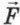 A уравновешивает силу тяжести
A уравновешивает силу тяжести 
 12. В воде и керосине плавают одинаковые деревянные шарики. На какой шарик действует бо´льшая сила Архимеда?
12. В воде и керосине плавают одинаковые деревянные шарики. На какой шарик действует бо´льшая сила Архимеда?