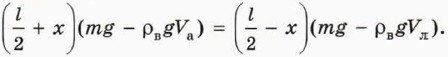|
|
|
|
|
|
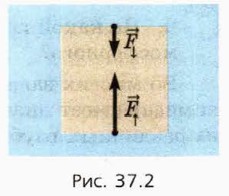
§ 37. Гидростатика Закон АрхимедаРассмотрим силы давления жидкости на погружённый в жидкость куб (рис. 37.2).
Силы давления на боковые грани куба взаимно уравновешиваются. Но силы давления на верхнюю и нижнюю грани не уравновешиваются: поскольку давление жидкости увеличивается с глубиной, на нижнюю грань куба действует большая сила давления, чем на верхнюю. Следовательно, равнодействующая сил давления, действующих на все участки поверхности куба, направлена вверх. Это — выталкивающая сила, или сила Архимеда, знакомая вам из курса физики основной школы.
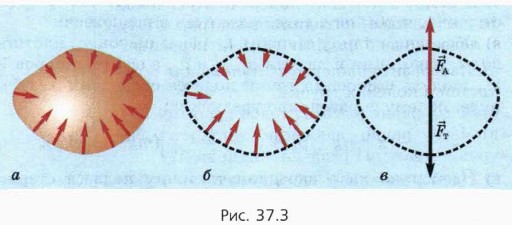
Найдём, чему равен модуль силы Архимеда, действующей на тело произвольной формы, куда эта сила направлена и в какой точке приложена. На рисунке 37.3, а красными стрелками схематически изображены силы давления жидкости, действующие на участки тела одинаковой площади. С увеличением глубины эти силы увеличиваются.
Мысленно заменим погружённое в жидкость тело этой же жидкостью. На участки поверхности этого «жидкого» тела будут действовать такие же силы давления, что и на данное тело (рис. 37.3, б). Следовательно, равнодействующая сил давления, действующая на жидкость в объёме данного тела, будет такой же, как и сила Архимеда, действующая на само данное тело. Заметим теперь, что выделенный объём жидкости находится внутри той же жидкости в равновесии. Следовательно, действующие на него сила тяжести
Приведённый вывод показывает, что сила Архимеда приложена в центре тяжести вытесненного телом объёма жидкости (рис. 37.3, в). Полученное выражение для силы Архимеда и утверждение о точке её приложения справедливы и тогда, когда тело погружено в жидкость лишь частично.
а) Сохранится ли равновесие стержня? И если нет, то какой шар в воде перевесит? б) В сторону какого шара надо передвинуть точку подвеса стержня, чтобы он в воде находился в равновесии? в) Обозначим длину стержня l, массы шаров m, плотности воды, алюминия и латуни ρв, ρа и ρл, а объёмы шаров Vа и Vл. Модуль смещения точки подвеса обозначим х. Объясните, почему справедливо уравнение:
г) Насколько надо передвинуть точку подвеса стержня, чтобы он в воде находился в равновесии, если l = 1 м, плотность латуни в 3 раза больше плотности алюминия, а плотность алюминия в 2,7 раза больше плотности воды?
|
|
|



 5. Чему равна сила Архимеда, действующая на куб с длиной ребра а, погружённый в жидкость плотностью ρ?
5. Чему равна сила Архимеда, действующая на куб с длиной ребра а, погружённый в жидкость плотностью ρ?
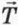 T и сила Архимеда
T и сила Архимеда