|
|
|
|
|
§ 11. Движение тела, брошенного горизонтально и под углом к горизонту Движение тела, брошенного под углом к горизонтуНа рисунке 11.3 схематически изображено начальное положение тела, его начальная скорость
Проекции начальной скорости υ0x = υ0cos α, (9) υ0y = υ0sin α. (10) Для сокращения последующих записей и прояснения их физического смысла удобно до получения окончательных формул сохранять обозначения υ0x и υ0y. Скорость и тела в векторном виде в момент времени (ив этом случае выражается формулой
Однако теперь в проекциях на оси координат
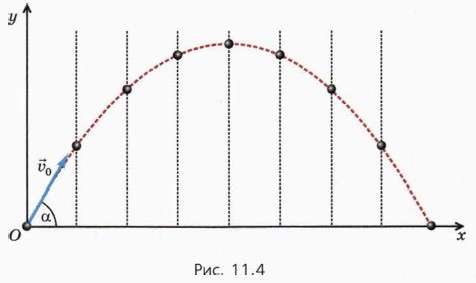
Мы видим, что и в этом случае брошенное тело как бы участвует одновременно в двух видах движения: вдоль оси х оно движется равномерно, а вдоль оси у — равноускоренно с начальной скоростью, как тело, брошенное вертикально вверх. Траектория движенияНа рисунке 11.4 схематически показано положение тела, брошенного под углом к горизонту, через равные промежутки времени. Вертикальные линии подчёркивают, что вдоль оси х тело движется равномерно: соседние линии находятся на равных расстояниях друг от друга.
Формула (15) представляет собой уравнение параболы, ветви которой направлены вниз. Уравнение траектории может многое рассказать нам о движении брошенного тела!
|
|
|



 0 (при t = 0) и ускорение (ускорение свободного падения
0 (при t = 0) и ускорение (ускорение свободного падения 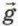 ).
).
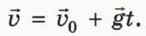

 7. Объясните, как получаются следующие уравнения:
7. Объясните, как получаются следующие уравнения: