Упругие столкновения (окончание)

11. Шар налетел со скоростью 2 м/с на второй покоящийся шар и отскочил назад со скоростью 0,5 м/с. Столкновение было упругим и центральным.

а) С какой скоростью начал двигаться второй шар после столкновения?

б) Чему равно отношение масс шаров?

П о д с к а з к а. Воспользуйтесь системой уравнений (3) и (4).

Столкновение подвешенных шаров

Упругие столкновения удобно исследовать с помощью подвешенных на нитях шаров.

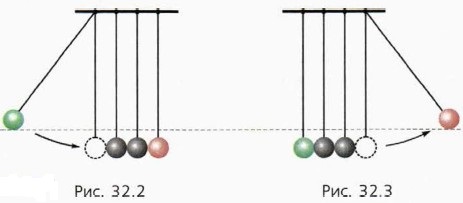
Подвесим на нитях равной длины несколько одинаковых стальных или костяных шаров (рис. 32.2).
Отведём в сторону крайний левый шар и отпустим. Мы окажемся свидетелями красивого явления. После удара левого шара все шары, кроме крайнего правого, будут находиться в покое, а крайний правый шар отклонится, поднявшись при этом на высоту, равную начальной высоте левого шара (рис. 32.3).

Рис. 32.2

12. Объясните описанный опыт, считая столкновение шаров упругим и центральным. Что будет наблюдаться, если отклонить не один, а два или три шара вместе? Проверьте своё предсказание на опыте.

Рассмотрим теперь случай, когда массы подвешенных шаров не равны.

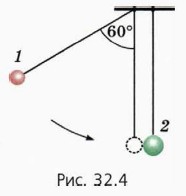
13. На вертикальных нитях длиной l = 90 см висят, соприкасаясь, два шарика массой m₁ = 20 г и m₂ = 40 г. Первый шарик отклонили так, что нить составила угол 60° с вертикалью, и отпустили без толчка (рис. 32.4). Столкновение шаров считайте упругим и центральным.

Рис. 32.4

а) Чему равна кинетическая энергия первого шарика перед столкновением?

б) Чему равна скорость первого шарика перед столкновением?

в) Чему равна скорость первого шарика после столкновения?

г) На какую максимальную высоту поднимется первый шарик после столкновения?

д) Чему равна скорость второго шарика после столкновения?

е) На какую максимальную высоту поднимется второй шарик после столкновения?

<<< К началу