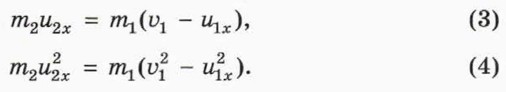|
|
|
|
|
|
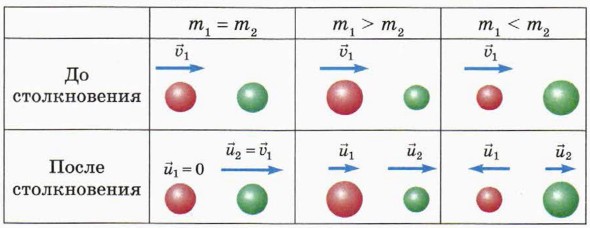
§ 32. Разрывы и столкновения Упругие столкновенияСтолкновение тел называют упругим, если механическая энергия тел в результате столкновения не изменяется. Таким можно считать, например, рассмотренное выше столкновение бильярдных шаров. Столкновение двух тел называют центральным, если их скорости до столкновения и после него направлены вдоль одной прямой. Пусть шар массой m1 движущийся со скоростью 1 В таком случае проекция скорости
П о д с к а з к а. До и после столкновения тела движутся вдоль оси х, поэтому квадраты скоростей равны квадратам проекций скоростей: Переход к системе двух линейных уравненийПерепишем уравнения (1) и (2) так, чтобы величины, относящиеся ко второму шару, находились слева от знака равенства, а к первому шару — справа. Кроме того, сократим общий множитель
u2x = υ1 + u1x. (5) П о д с к а з к а. Если столкновение произошло, то обе части уравнения (3) отличны от нуля. Поэтому можно разделить левую и правую части уравнения (4) соответственно на левую и правую части уравнения (3). Уравнения (3) и (5) представляют собой систему двух линейных уравнений. Используя эту систему, легко выполнить следующее задание.
Из формул, полученных при выполнении этого задания, можно сделать качественные выводы, которые помогут при решении задач.
|
|
|



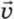 1, налетает на покоящийся шар массой m2. Обозначим
1, налетает на покоящийся шар массой m2. Обозначим  1 и
1 и  7. Объясните смысл следующих уравнений:
7. Объясните смысл следующих уравнений:
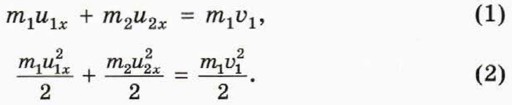
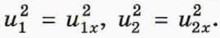
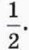 Мы получим:
Мы получим: