Гладкая горка и шайба (продолжение)

Рассмотрим теперь кратко оставшиеся варианты.

Пусть реализуется первый вариант: шайба не достигла вершины горки и соскользнула обратно, см. рисунок 34.2. В таком случае для нахождения значений конечной скорости горки и шайбы их можно рассматривать как тела, между которыми произошло упругое столкновение (см. § 32).

Действительно, в конечном состоянии шайба снова скользит по столу, поэтому её потенциальная энергия не изменилась по сравнению с начальной. Следовательно, сохранилась и суммарная кинетическая энергия горки и шайбы. Кроме того, сохранился и их суммарный импульс.

Начальную скорость шайбы можно найти, зная максимальную высоту, до которой она поднялась по горке.

5. На покоящуюся гладкую горку массой 1 кг и высотой 15 см налетает слева шайба массой 300 г. Шайба достигает максимальной высоты 10 см.

а) Какова начальная скорость шайбы?

б) Чему равна общая скорость горки и шайбы в момент, когда шайба остановится относительно горки?

в) Чему равны конечные скорости горки и шайбы и как они направлены?

П о д с к а з к а. В момент, когда шайба достигла максимальной высоты, её скорость относительно стола равна скорости горки и направлена горизонтально.

Рассмотрим наконец третий вариант, когда шайба преодолевает горку и скользит по столу дальше.

6. Объясните, почему в этом случае конечная скорость шайбы равна её начальной скорости, а конечная скорость горки равна нулю.

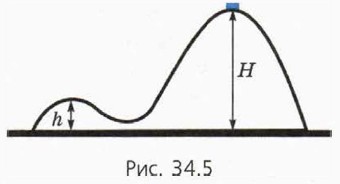
П о д с к а з к а. Это — единственное решение системы уравнений, выражающих законы сохранения энергии и импульса, если шайба в конечном состоянии находится по другую сторону горки.

Итак, поднимаясь на горку, шайба разгоняет её, а спускаясь по другому склону, тормозит горку до остановки.

Горка с двумя вершинами

Возьмём теперь гладкую горку массой М с двумя вершинами высотой Н и h (рис. 34.5). На более высокой из них в начальном состоянии покоится шайба массой m. Шайба начинает соскальзывать влево. При движении тел шайба не отрывалась от горки, а горка — от гладкого стола.

Рис. 34.5

7. Какие физические величины сохраняются в данном случае?

8. Запишите систему уравнений, выражающую законы сохранения, для момента, когда шайба будет на вершине высотой h. Какие величины можно найти с помощью этой системы? Выразите эти величины через приведённые выше.

9. Чему равны скорости горки и шайбы, когда шайба находится на второй вершине горки, если М = 100 г, m = 20 г, Н = 8 см, h = 2 см (см. рис. 34.5)? Как будут направлены эти скорости?

<<< К началу Окончание >>>