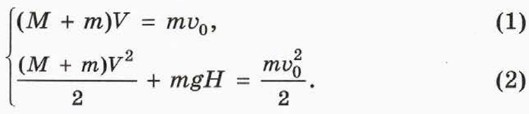|
|
|
|
|
|
§ 34. Движение системы тел Гладкая горка и шайбаГорка с одной вершинойПусть на гладком столе покоится гладкая горка массой М и высотой Н (рис. 34.1). На неё налетает со скоростью
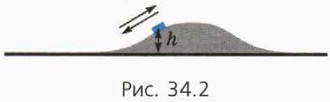
Возможны три варианта развития событий. 1) Шайба не достигнет вершины горки и соскользнёт по тому же склону (рис. 34.2).
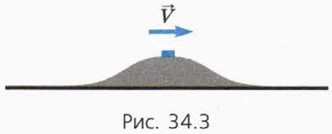
2) Шайба достигнет вершины горки в момент, когда их скорости относительно стола равны (рис. 34.3).
3) Шайба «перевалит» через вершину горки и соскользнёт по другому склону (рис. 34.4).
Второй вариант — «пограничный». Поэтому с него и начнём: выясним, при каких значениях М, Н, m, υ0 он реализуется.
П о д с к а з к а. Используя уравнение (1), выразите υ0 через М, m, V и подставьте в уравнение (2).
а) Чему равна начальная скорость шайбы, если М = 1 кг, m = 100 г, Н = 20 см? б) Чему равна высота горки, если υ0 = 3 м/с, а масса шайбы в 2 раза меньше массы горки? в) Чему равна масса шайбы, если υ0 = 1 м/с, М = 2 кг, Н = 4 см?
|
|
|



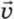 0 шайба массой m. Двигаясь по горке, шайба не отрывается от неё.
0 шайба массой m. Двигаясь по горке, шайба не отрывается от неё.

 1. Объясните, почему в случае, когда горка и шайба в результате взаимодействия движутся как единое целое со скоростью
1. Объясните, почему в случае, когда горка и шайба в результате взаимодействия движутся как единое целое со скоростью 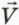 , справедливы уравнения
, справедливы уравнения