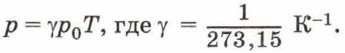|
|
|
|
|
Глава 6. Свойства газов Газовые законыЗакон Гей-Люссака иногда записывают иначе. Предположим, что газ переводят из состояния при нормальных условиях (р0 — нормальное атмосферное давление, Т0 = 273,15 К, V0 — соответствующий объём) в состояние с параметрами Т и V. Тогда закон Гей-Люссака запишется следующим образом:
Обозначив
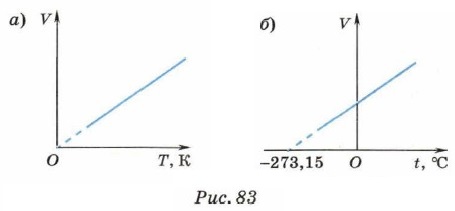
Коэффициент α называют температурным коэффициентом объёмного расширения газа. Он одинаков для всех газов и показывает, что при нагревании на 1 К объём газа увеличивается на 1/273,15 часть того объёма, который газ занимал при 273,15 К (при 0 °С). Напомним, что термодинамическая температура и температура по шкале Цельсия связаны соотношением: T = t + 273,15. Тогда формула закона Гей-Люссака будет иметь вид: V = V0α(t + 273,15). Учитывая, что V=V0(1 + αt). Зависимость объёма газа данной массы от температуры при постоянном давлении является линейной; график этой зависимости — прямая, называемая изобарой (рис. 83).
На рисунке 83, а приведён график зависимости объёма от термодинамической температуры, а на рисунке 83, б — от температуры по шкале Цельсия. В первом случае график должен проходить через начало координат (при Т = 0, V = 0). Однако при низких температурах газ нельзя считать идеальным, поэтому график проводят пунктиром. Реальные газы при низких температурах превращаются в жидкости, а к жидкостям уравнение Клапейрона так же, как и закон Гей-Люссака, неприменимо. Во втором случае график должен был бы пересечь ось абсцисс в точке t = -273,15 °С. Согласно молекулярно-кинетической теории строения вещества при увеличении температуры увеличивается средняя кинетическая энергия теплового движения молекул газа и, следовательно, увеличивается давление газа на стенки сосуда. Для того чтобы оно осталось неизменным (изобарный процесс), должна уменьшиться концентрация молекул. Это и происходит при увеличении объёма газа при его неизменной массе. При изобарном процессе переданное системе количество теплоты расходуется и на изменение внутренней энергии системы, и на совершение системой работы против внешних сил: Q = ΔU + pΔV. Если газу передаётся некоторое количество теплоты, то он расширяется (ΔV > 0 и pΔV > 0) и его внутренняя энергия возрастает (ΔU > 0), газ нагревается (ΔТ > 0). Если газ отдаёт некоторое количество теплоты (Q < 0), то он сжимается (ΔV < 0) и его внутренняя энергия уменьшается (ΔU < 0), газ охлаждается (ΔТ < 0). Изохорный процесс4. Нагревая газ в закрытом сосуде с абсолютно твёрдыми стенками, можно осуществить процесс, происходящий при неизменном объёме.
Запишем уравнение Клапейрона: Учитывая, что V1 = V2, получим:
или
Этот закон был открыт французским учёным Жаком Александром Цезаром Шарлем (1746—1823) в 1787 г. и носит его имя. Закон Шарля так же, как и закон Гей-Люссака, может быть записан иначе. Если газ переводится из состояния при нормальных условиях в состояние с параметрами р и Т и при этом масса газа остаётся неизменной, то можно записать:
Обозначив
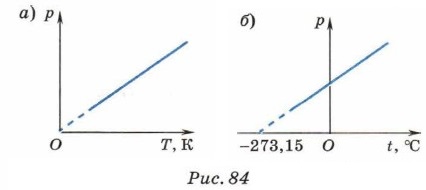
Коэффициент γ называют температурным коэффициентом давления газа. Он одинаков для всех газов и показывает, что при нагревании на 1 К давление газа увеличивается на 1/273,15 часть того давления, которое производил газ при нормальных условиях. Выражая температуру в градусах Цельсия, можно записать: р = р0(1 + γt). Графиком зависимости давления газа данной массы от температуры является прямая, называемая изохорой (рис. 84). График на рисунке 84, а должен был бы проходить через начало координат, однако при низких температурах применить к газу закон Шарля уже нельзя.
Согласно молекулярно-кинетической теории строения вещества при повышении температуры увеличивается средняя кинетическая энергия хаотического движения молекул, а следовательно, при неизменной концентрации молекул увеличивается давление газа. При изохорном процессе объём газа не изменяется, поэтому работа системы против внешних сил равна нулю. Первый закон термодинамики для изохорного процесса имеет вид: Q = ΔU, т. е. всё переданное системе количество теплоты идёт на увеличение её внутренней энергии. Закон Шарля так же, как и другие газовые законы, записан для идеального газа и применим только в тех случаях, когда реальный газ по своим свойствам близок к идеальному.
|
|
|



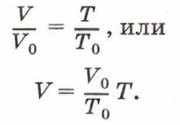
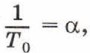 получим:
получим:
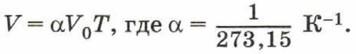
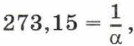 запишем
запишем
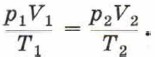
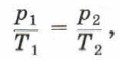

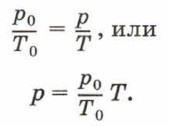
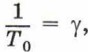 получим:
получим: