|
|
|
|
|
Глава 5. Закон сохранения энергии § 44. Потенциальная энергияВспомните, какая связь существует между работой силы тяжести и потенциальной энергией. Почему работа силы упругости определяется её средним значением? Согласно теореме об изменении кинетической энергии работа силы, действующей на тело, равна изменению его кинетической энергии:
Если же силы взаимодействия между телами являются консервативными, то, используя явные выражения для сил, мы показали (см. § 43), что работу таких сил можно также представить в виде разности двух значений некоторой величины, зависящей от взаимного расположения тел (или частей одного тела):
Здесь высоты h1 и h2 определяют взаимное расположение тела и поверхности Земли, а удлинения х1 и х2 — взаимное расположение частей тела, например витков деформированной пружины. Из формул (5.18) и (5.19) следует, что
Введя понятие потенциальной энергии, мы получаем возможность выразить работу любых консервативных сил через изменение потенциальной энергии. Под изменением величины понимают разность между её конечным и начальным значениями, поэтому Еп = Еп2 - Еп1. Следовательно, оба уравнения (5.19) можно записать так: А = Еп1 — Еп2 = -(Еп2 — Еп1) = -ΔЕп, (5.22) откуда ΔЕп = -А.
Например, при падении камня на Землю его потенциальная энергия убывает (ΔЕп < 0), но сила тяжести совершает положительную работу (А > 0). Следовательно, А и ΔЕп имеют противоположные знаки в соответствии с формулой (5.22). Нулевой уровень потенциальной энергии. Согласно уравнению (5.22) работа консервативных сил определяет не саму потенциальную энергию, а её изменение. Поскольку работа определяет лишь изменение потенциальной энергии, то только изменение энергии в механике имеет физический смысл. Поэтому
Ни одно явление в природе или технике не определяется значением самой потенциальной энергии. Важна лишь разность значений потенциальной энергии в конечном и начальном состояниях системы тел. Выбор нулевого уровня производится по-разному и диктуется условиями данной задачи. Обычно в качестве состояния с нулевой потенциальной энергией выбирают состояние системы с минимальным значением энергии. Тогда потенциальная энергия всегда положительна или равна нулю. Итак, потенциальная энергия системы «тело — Земля» — величина, зависящая от положения тела относительно Земли, равная работе консервативной силы при перемещении тела из точки, где оно находится, в точку, соответствующую нулевому уровню потенциальной энергии системы. У пружины потенциальная энергия минимальна в отсутствие деформации, а у системы «камень — Земля» — когда камень лежит на поверхности Земли. Поэтому в первом случае Но к данным выражениям можно добавить любую постоянную величину С. При этом изменение потенциальной энергии, определяемое работой консервативной силы, останется прежним.
Если не удерживать тело, то оно падает на землю (h = 0); если отпустить растянутую или сжатую пружину, то она вернётся в недеформированное состояние (х = 0). Вопросы к параграфу 1. В чём состоит сходство кинетической энергии тела с потенциальной? 2. В чём состоит различие между кинетической энергией и потенциальной? 3. Может ли потенциальная энергия быть отрицательной?
|
|
|






 Приведите примеры выбора нулевого уровня отсчёта потенциальной энергии, относительно которого потенциальная энергия тела будет иметь отрицательные значения.
Приведите примеры выбора нулевого уровня отсчёта потенциальной энергии, относительно которого потенциальная энергия тела будет иметь отрицательные значения.
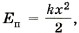 а во втором случае Еп = mgh.
а во втором случае Еп = mgh.