|
|
|
|
|
Глава 5. Закон сохранения энергии § 45. Закон сохранения энергии в механикеКак изменяются потенциальная, кинетическая и полная механическая энергии тела при его свободном падении вниз? если тело брошено вверх? Обратимся к простой системе тел, состоящей из земного шара и поднятого над поверхностью Земли тела, например камня. Камень падает под действием силы тяжести. Силу сопротивления воздуха учитывать не будем. Изменение кинетической энергии камня равно работе сил тяжести: ΔЕк = Aт (5.23) Изменение потенциальной энергии равно работе силы тяжести, взятой с обратным знаком: ΔЕп = -Ат (5.24) Работа силы тяжести, действующей со стороны камня на земной шар, практически равна нулю. Из-за большой массы земного шара его перемещением и изменением скорости можно пренебречь. Из формул (5.23) и (5.24) следует, что ΔЕк = -ΔЕп. (5.25) Равенство (5.25) означает, что увеличение кинетической энергии системы равно убыли её потенциальной энергии (или наоборот). Отсюда следует, что ΔЕк + ΔЕп = 0, или Δ (Ек + Еп) = 0. (5.26) Изменение суммы кинетической и потенциальной энергий системы равно нулю. Полная механическая энергия Е равна сумме кинетической и потенциальной энергий тел, входящих в систему: Е = Ек + Еп. (5.27) Так как изменение полной энергии системы в рассматриваемом случае согласно уравнению (5.26) равно нулю, то энергия остаётся постоянной: Е = Ек + Еп = const. (5.28)
Закон сохранения механической энергии является частным случаем общего закона сохранения энергии.
Учитывая, что в рассматриваемом конкретном случае Еп = mgh и
или
Это уравнение позволяет очень просто найти скорость υ2 камня на любой высоте h2 над землёй, если известна начальная скорость камня на исходной высоте h1.
Закон сохранения механической энергии (5.28) легко обобщается на случай любого числа тел и любых консервативных сил взаимодействия между ними. Под Ек нужно понимать сумму кинетических энергий всех тел, а под Еп — полную потенциальную энергию системы. Для системы, состоящей из тела массой m и горизонтально расположенной пружины (см. рис. 5.13), закон сохранения механической энергии имеет вид
Уменьшение механической энергии системы под действием сил трения. Рассмотрим влияние сил трения на изменение механической энергии системы. Если в изолированной системе силы трения совершают работу при движении тел относительно друг друга, то её механическая энергия не сохраняется. В этом легко убедиться, толкнув книгу, лежащую на столе. Из-за действия силы трения книга почти сразу останавливается. Сообщённая ей механическая энергия исчезает. Сила трения совершает отрицательную работу и уменьшает кинетическую энергию. Но потенциальная энергия при этом не увеличивается. Поэтому полная механическая энергия убывает. Кинетическая энергия не превращается в потенциальную.
Силы трения (сопротивления) неконсервативны. Отличие сил трения от консервативных сил становится особенно наглядным, если рассмотреть работу тех и других на замкнутом пути. Работа силы тяжести, например, на замкнутом пути всегда равна нулю. Она положительна при падении тела с высоты h и отрицательна при подъёме на ту же высоту. Работа же силы сопротивления воздуха отрицательна как при подъёме тела вверх, так и при движении его вниз. Поэтому на замкнутом пути она обязательно меньше нуля. В любой системе, состоящей из больших макроскопических тел, действуют силы трения. Следовательно, даже в изолированной системе движущихся тел механическая энергия обязательно убывает. Постепенно затухают колебания маятника, останавливается машина с выключенным двигателем и т. д. Но убывание механической энергии не означает, что эта энергия исчезает бесследно. В действительности происходит переход энергии из механической формы в другие. Обычно при работе сил трения происходит нагревание тел, или, как говорят, увеличение их внутренней энергии. Во всех процессах, происходящих в природе, как и в создаваемых приборах, устройствах, всегда выполняется закон сохранения и превращения энергии: энергия не исчезает и не появляется вновь, она может только перейти из одного вида в другой.
Вопросы к параграфу 1. Что называется полной механической энергией системы? 2. Может ли сохраняться механическая энергия системы, на которую действуют внешние силы? 3. Тело падает с высоты Н. Постройте графики зависимости потенциальной, кинетической и полной энергий системы «тело—Земля» от высоты h. Все высоты считайте от поверхности Земли. 4. В каких случаях механическая энергия системы сохраняется? 5. Почему сила трения является неконсервативной? 6. Во что переходит механическая энергия в системе, в которой действуют силы трения?
|
|
|



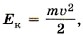 закон сохранения механической энергии можно записать так:
закон сохранения механической энергии можно записать так:

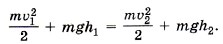
 Чем мы пренебрегаем, когда говорим, что механическая энергия падающего камня сохраняется? Какие превращения энергии реально происходят при падении камня в воздухе?
Чем мы пренебрегаем, когда говорим, что механическая энергия падающего камня сохраняется? Какие превращения энергии реально происходят при падении камня в воздухе?

 Нагревание при действии сил трения легко обнаружить. Для этого, например, достаточно энергично потереть монету о стол. С повышением температуры, как известно из курса физики основной школы, повышается кинетическая энергия теплового движения молекул или атомов. Следовательно, при действии сил трения кинетическая энергия тела превращается в кинетическую энергию хаотично движущихся молекул.
Нагревание при действии сил трения легко обнаружить. Для этого, например, достаточно энергично потереть монету о стол. С повышением температуры, как известно из курса физики основной школы, повышается кинетическая энергия теплового движения молекул или атомов. Следовательно, при действии сил трения кинетическая энергия тела превращается в кинетическую энергию хаотично движущихся молекул.