|
|
|
|
|
Глава 5. Закон сохранения энергии § 46. Работа силы тяготения. Потенциальная энергия в поле тяготенияВ чём выражается гравитационное взаимодействие тел? Как доказать наличие взаимодействия Земли и, например, учебника физики? В § 43 мы рассмотрели работу силы тяжести и выяснили, что сила тяжести — консервативная сила. Теперь найдём выражение для работы силы тяготения и докажем, что работа этой силы не зависит от формы траектории, т. е. что сила тяготения также консервативная сила. Напомним, что работа консервативной силы по замкнутому контуру равна нулю. Пусть тело массой m находится в поле тяготения Земли. Очевидно, что размеры этого тела малы по сравнению с размерами Земли, поэтому его можно считать материальной точкой. На тело действует сила тяготения
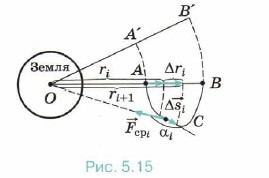
где G — гравитационная постоянная, М — масса Земли, r — расстояние, на котором находится тело от центра Земли. Пусть тело перемещается из положения А в положение В по разным траекториям: 1) по прямой АВ; 2) по кривой АА'В'В; 3) по кривой АСВ (рис. 5.15) 1. Рассмотрим первый случай. Сила тяготения, действующая на тело, непрерывно уменьшается, поэтому рассмотрим работу этой силы на малом перемещении Δri = ri + 1 — ri. Среднее значение силы тяготения равно:
Чем меньше Δri, тем более справедливо написанное выражение r2сpi = riri + 1.
Тогда работу силы Fсpi, на малом перемещении Δri, можно записать в виде
Суммарная работа силы тяготения при перемещении тела из точки А в точку В равна:
2. При движении тела по траектории АА'В'В (см. рис. 5.15) очевидно, что работа силы тяготения на участках АА' и В'В равна нулю, так как сила тяготения направлена к точке О и перпендикулярна любому малому перемещению по дуге окружности. Следовательно, работа будет также определяться выражением (5.31). 3. Определим работу силы тяготения при движении тела от точки А к точке В по траектории АСВ (см. рис. 5.15). Работа силы тяготения на малом перемещении Δsi равна ΔАi = FсрiΔsicosαi,.. Из рисунка видно, что Δsicosαi = - Δri, и суммарная работа опять же будет определяться по формуле (5.31). Итак, можно сделать вывод, что А1 = А2 = А3, т. е. что работа силы тяготения не зависит от формы траектории. Очевидно, что работа силы тяготения при перемещении тела по замкнутой траектории АА'В'ВА равна нулю.
Изменение потенциальной энергии равно работе силы тяготения, взятой с обратным знаком: Если выбрать нулевой уровень потенциальной энергии на бесконечности, т. е. ЕпВ = 0 при rВ → ∞, то Потенциальная энергия тела массой m, находящегося на расстоянии r от центра Земли, равна:
Закон сохранения энергии для тела массой m, движущегося в поле тяготения, имеет вид
где υ1 — скорость тела на расстоянии r1 от центра Земли, υ2 — скорость тела на расстоянии r2 от центра Земли. Определим, какую минимальную скорость надо сообщить телу вблизи поверхности Земли, чтобы оно в отсутствие сопротивления воздуха могло удалиться от неё за пределы сил земного притяжения.
На тело со стороны Земли действует сила тяготения, которая зависит от расстояния центра масс этого тела до центра масс Земли. Поскольку неконсервативных сил нет, полная механическая энергия тела сохраняется. Внутренняя потенциальная энергия тела остаётся постоянной, так как оно не деформируется. Согласно закону сохранения механической энергии
На поверхности Земли тело обладает и кинетической, и потенциальной энергией:
где υII — вторая космическая скорость, М3 и Я3 — соответственно масса и радиус Земли. В бесконечно удаленной точке, т. е. при r → ∞, потенциальная энергия тела равна нулю (Wп = 0), а так как нас интересует минимальная скорость, то и кинетическая энергия также должна быть равна нулю: Wк = 0. Из закона сохранения энергии следует:
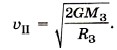
отсюда
Эту скорость можно выразить через ускорение свободного падения вблизи поверхности Земли (при расчётах, как правило, этим выражением пользоваться удобнее). Поскольку Следовательно, искомая скорость
Точно такую же скорость приобрело бы тело, упавшее на Землю с бесконечно большой высоты, если бы не было сопротивления воздуха. Заметим, что вторая космическая скорость в
Вопросы к параграфу 1. Является ли сила тяготения консервативной? Почему? 2. Какие физические величины остаются постоянными, а какие изменяются при расчёте второй космической скорости? 3. Изменится ли значение второй космической скорости, если ракету запустить из глубокой шахты? 4. Как изменится выражение для потенциальной энергии тела в поле тяготения, если за нулевой уровень её отсчёта взять поверхность Земли?
|
|
|



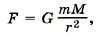
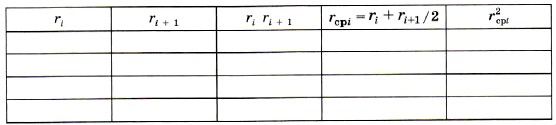
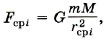 где r2сpi = riri + 1.
где r2сpi = riri + 1.
 Проверьте это утверждение, подставляя разные числа.
Проверьте это утверждение, подставляя разные числа.
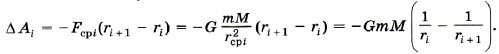
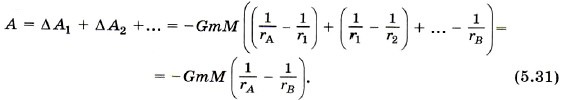
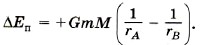
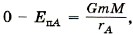 следовательно,
следовательно, 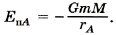
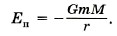
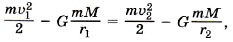
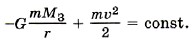
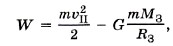
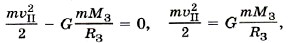
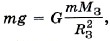 то GM3 = gR23.
то GM3 = gR23.
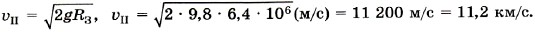
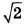 раза больше, чем первая.
раза больше, чем первая.