Главная >> Физика 10 класс. Мякишев

Глава 10. Уравнение состояния идеального газа. Газовые законы

§ 65. Газовые законы

Вспомните, состояние какого газа описывает уравнение Менделеева—Клапейрона.

Можно ли универсальную газовую постоянную считать фундаментальной постоянной?

С помощью уравнения состояния идеального газа можно исследовать процессы, в которых масса газа и один из трёх параметров — давление, объём или температура — остаются неизменными.

Запомни Количественные зависимости между двумя параметрами газа при фиксированном значении третьего называют газовыми законами. Процессы, протекающие при неизменном значении одного из параметров, называют изопроцессами.

Слово «изопроцесс» — сложное слово, первая часть которого происходит от греческого слова isos — равный, одинаковый.

Отметим, что в действительности ни один процесс не может протекать при строго фиксированном значении какого-либо параметра. Всегда имеются те или иные воздействия, нарушающие постоянство температуры, давления или объёма. Лишь в лабораторных условиях удаётся поддерживать постоянство того или иного параметра с высокой точностью, но в действующих технических устройствах и в природе это практически неосуществимо. Изопроцесс — это идеализированная модель реального процесса, которая только приближённо отражает действительность.

Изотермический процесс.

Запомни Процесс изменения состояния системы макроскопических тел (термодинамической системы) при постоянной температуре называют изотермическим.

Слово «изотермический» происходит от греческих слов isos — равный, одинаковый и therme — теплота.

Для поддержания температуры газа постоянной необходимо, чтобы он мог обмениваться теплом с большой системой — термостатом. Иначе при сжатии или расширении температура газа будет меняться. Термостатом может служить атмосферный воздух, если температура его заметно не меняется на протяжении всего процесса. Согласно уравнению состояния идеального газа (10.4), если масса газа не изменяется, в любом состоянии с неизменной температурой произведение давления газа на его объём остаётся постоянным:

pV = const при Т = const.                     (10.6)

Этот вывод был сделан английским учёным Р. Бойлем (1627—1691) и несколько позже французским учёным Э. Мариоттом (1620—1684) на основе эксперимента. Поэтому он носит название закона Бойля—Mapuoттa.

Закона Бойля—Mapuoттa Для газа данной массы при рдение давления газа на его объём постоянно.

Закон Бойля—Мариотта справедлив обычно для любых газов, а также и для их смесей, например для воздуха. Лишь при давлениях, в несколько сотен раз больших атмосферного, отклонения от этого закона становятся существенными.

Запомни Кривую, изображающую зависимость давления газа от объёма при постоянной температуре, называют изотермой.

Начертите изотермы в осях р, Т и V, Т.

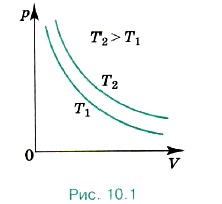
Изотерма газа изображает обратно пропорциональную зависимость между давлением и объёмом. Кривую такого рода в математике называют гиперболой (рис. 10.1).

Различным постоянным температурам соответствуют различные изотермы. При повышении температуры газа давление согласно уравнению состояния (10.4) увеличивается, если V = const. Поэтому изотерма, соответствующая более высокой температуре Т₂, лежит выше изотермы, соответствующей более низкой температуре Т₁ (см. рис. 10.1).

Для того чтобы процесс происходил при постоянной температуре, сжатие или расширение газа должно происходить очень медленно. Дело в том, что, например, при сжатии газ нагревается, так как при движении поршня в сосуде скорость и соответственно кинетическая энергия молекул после ударов о поршень увеличиваются, а следовательно, увеличивается и температура газа. Именно поэтому для реализации изотермического процесса надо после небольшого смещения поршня подождать, когда температура газа в сосуде опять станет равной температуре окружающего воздуха.

Кроме этого, отметим, что при быстром сжатии давление под поршнем сразу становится больше, чем во всём сосуде. Если значения давления и температуры в различных точках объёма разные, то в этом случае газ находится в неравновесном состоянии и мы не можем назвать значения температуры и давления, определяющие в данный момент состояние системы. Если систему предоставить самой себе, то температура и давление постепенно выравниваются, система приходит в равновесное состояние.

Запомни Равновесное состояние — это состояние, при котором температура и давление во всех точках объёма одинаковы.

Параметры состояния газа могут быть определены, если он находится в равновесном состоянии.

Запомни Процесс, при котором все промежуточные состояния газа являются равновесными, называют равновесным процессом.

Очевидно, что на графиках зависимости одного параметра от другого мы можем изображать только равновесные процессы.

Окончание параграфа >>>