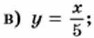|
|
|
|
|
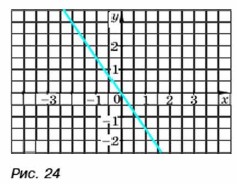
§ 6. Линейная функция Прямая пропорциональность и её график (продолжение)Рассуждая аналогично, можно построить, например, график функции у = -1,5х (рис. 24). Этот график, так же как и график функции у 0,5х, является прямой и проходит через начало координат.
Вообще,
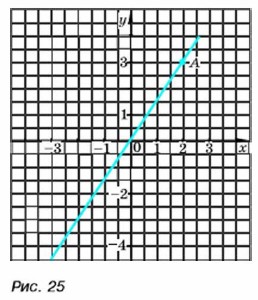
Чтобы построить график функции у = kх, достаточно найти координаты какой-нибудь точки графика этой функции, отличной от начала координат, отметить эту точку и через неё и начало координат провести прямую. Построим, например, график функции у = 1,5x. Пусть x = 2, тогда у = 3. Построим точку A(2; 3) и через неё и начало координат проведём прямую. Эта прямая является графиком функции у = 1,5x (рис. 25).
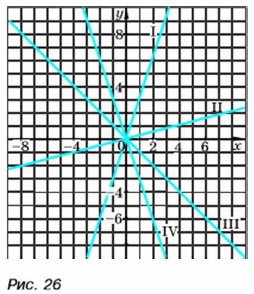
Расположение графика функции у = kx в координатной плоскости зависит от коэффициента k. Из формулы у = kx находим, что если x = 1, то у = k. «Значит, график функции у = kх проходит через точку (1; k). При k > 0 эта точка расположена в первой координатной четверти, а при k < 0 — в четвёртой. Отсюда следует, что при k > 0 график прямой пропорциональности расположен в первой и третьей координатных четвертях, а при k < 0 — во второй и четвёртой. На рисунке 26 построены графики прямой пропорциональности при различных значениях k.
Упражнения 297. Велосипедист движется равномерно со скоростью 12 км/ч. Напишите формулу, выражающую зависимость пройденного пути s (в километрах) от времени движения t (в часах). Является ли эта зависимость прямой пропорциональностью? 298. Является ли прямой пропорциональностью функция, заданная формулой:
299. Прямая пропорциональность задана формулой Найдите значение у, соответствующее x, равному -9; 0; 1; 4. 300. Постройте график прямой пропорциональности, заданной формулой:
301. (Для работы в парах.) Задайте формулой прямую пропорциональность, график которой симметричен графику функции у = 9х: а) относительно оси х; б) относительно оси у. 1) Распределите, кто выполняет задание а), а кто — задание б), и выполните их. 2) Проверьте друг у друга правильность выполнения задания.
|
|
|