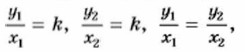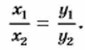Прямая пропорциональность и её график

Рассмотрим пример. Пусть V — объём железного бруска в кубических сантиметрах, m — его масса в граммах. Так как плотность железа равна 7,8 г/см³, то m = 7,8 V. Зависимость массы железного бруска от его объёма является примером функции, которая задаётся формулой вида у = kх, где х — независимая переменная, k — число, отличное от нуля.

Такую функцию называют прямой пропорциональностью.

Определение. Прямой пропорциональностью называется функция, которую можно задать формулой вида у = kх, где х — независимая переменная, k — не равное нулю число.

Число к в формуле у = kх называется коэффициентом прямой пропорциональности.

Из формулы у = kх, где k ≠ 0, находим, что если х₁ и х₂ — значения аргумента, причём х₁ ≠ 0, х₂ ≠ 0, а у₁ и у₂ — соответствующие им значения функции, то у₁ = kх₁, у₂ = kх₂. Отсюда

т. е. верна пропорция

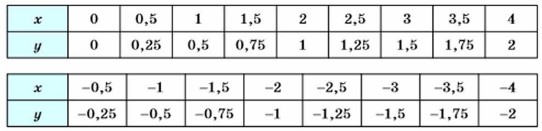
С этим и связано название «прямая пропорциональность» в отличие от «обратной пропорциональности», с которой вы познакомитесь позже.

В повседневной жизни мы часто встречаемся с зависимостями между переменными, которые являются прямыми пропорциональностями.

Приведём примеры.

Пример 1. Путь s км, пройденный автомобилем за t ч с постоянной скоростью 70 км/ч, вычисляется по формуле s = 70t, где t > 0, т. е. зависимость s от t является прямой пропорциональностью.

Пример 2. Стоимость р товара в рублях по цене 15 р. за килограмм вычисляется по формуле

р = 15x,

где х — масса товара в килограммах. Зависимость р от х является прямой пропорциональностью.

Пример 3. Длина окружности С вычисляется по формуле

С = 2πr,

где r — радиус окружности, π — число, приближённо равное 3,14. Значит, зависимость С от r является прямой пропорциональностью (коэффициент пропорциональности здесь равен 2π).

Выясним, что представляет собой график прямой пропорциональности.

В качестве примера рассмотрим функцию у = 0,5x и построим график этой функции.

Область определения функции у = 0,5х — множество всех чисел. Составим таблицу соответственных значений переменных х и у для некоторых значений аргумента х:

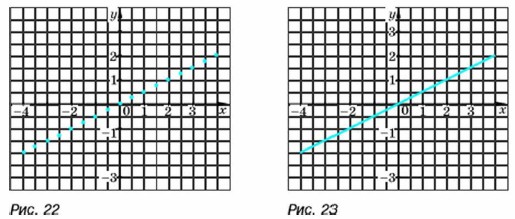
Отметим в координатной плоскости точки, координаты которых помещены в таблице (рис. 22). Можно заметить, что все отмеченные точки принадлежат некоторой прямой, проходящей через начало координат. Проведём эту прямую. Получим график функции у = 0,5x (рис. 23).

Продолжение >>>