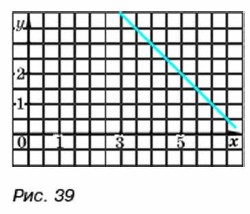
|
|
|
|
|
§ 6. Линейная функция
Линейная функция и её график (окончание)328. На рисунке 39 изображён график одной из линейных функций. Укажите эту функцию.
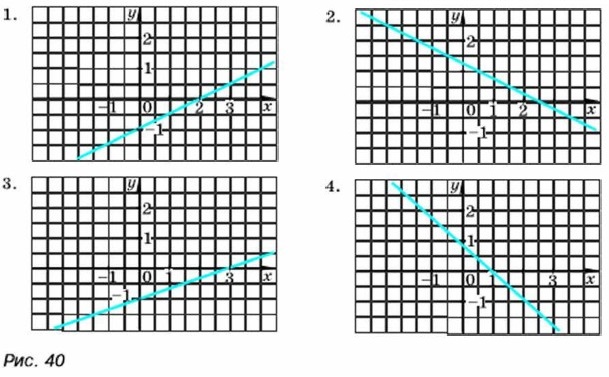
1. у = -2x + 6 2. у = x + 7 3. у = х - 7 4. у = -x + 7 329. Один из графиков на рисунке 40 является графиком функции
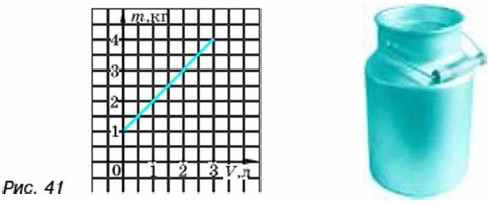
330. (Для работы в парах.) На рисунке 41 изображён график зависимости массы бидона с жидкостью от объёма жидкости. Найдите по графику: а) массу пустого бидона; б) массу бидона с одним литром жидкости; в) массу одного литра жидкости; г) объём жидкости в бидоне, если общая масса бидона с жидкостью равна 3 кг.
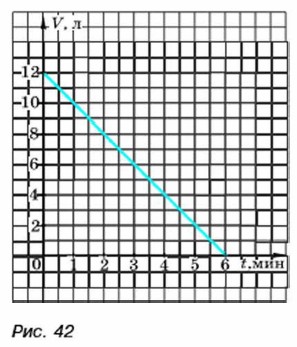
1) Выполните каждый задания а) и б). 2) Сравните полученные ответы. Исправьте ошибки, если они допущены. 3) Обсудите, как с помощью графика можно выполнить задания в) и г). 331. Из бака ёмкостью 12 л, наполненного доверху водой, равномерно вытекает вода. График зависимости V от t, где V — объём воды в баке (в литрах), a t — время вытекания воды (в минутах), построен на рисунке 42. Пользуясь графиком, найдите:
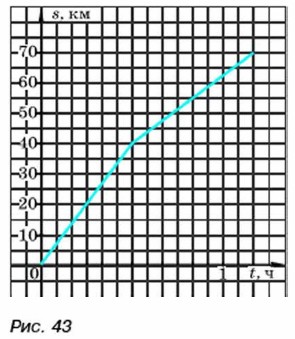
а) объём воды в баке через 3 мин; б) время, через которое в баке осталось 4 л воды; в) за какое время вытекла вся вода. 332. Дачник отправился из дома на автомобиле в посёлок. Сначала он ехал по шоссе, а затем по просёлочной дороге, сбавив при этом скорость. График движения дачника изображён на рисунке 43. Пользуясь графиком, ответьте на вопросы:
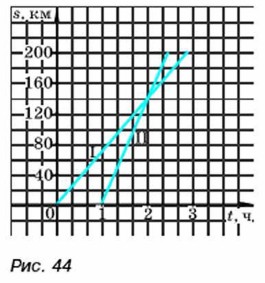
а) сколько времени ехал дачник по шоссе и сколько километров по шоссе он проехал; какая скорость автомобиля была на этом участке пути; б) сколько времени ехал дачник но просёлочной дороге и сколько километров он проехал но этой дороге; какова была скорость автомобиля на этом участке пути; в) за какое время дачник проехал весь путь от дома до посёлка? 333. В бак налили воду, температура которой 10 °С, и нагревали её до 100 °С, причём через каждую минуту температура повышалась на 1,5 °С. Задайте формулой зависимость температуры воды Т (в градусах Цельсия) от времени нагревания t (в минутах). Постройте график этой зависимости. Узнайте но графику: а) какую температуру имела вода через 5 мин; через 10 мин после начала нагревания; б) через какое время вода нагрелась до 85 °С. 334. Группа туристов отправилась со станции на турбазу. Первые 2 ч они шли со скоростью 4,5 км/ч. Затем сделали привал на 1 ч. На оставшуюся часть пути они затратили полтора часа, проходя её со скоростью 6 км/ч. Постройте график движения туристов. 335. (Для работы в парах.) На рисунке 44 изображены графики движения двух машин, следующих из города А в город В, расстояние между которыми 200 км. С помощью этих графиков ответьте на вопросы: а) какое время была в пути первая машина; вторая машина; б) какая машина начала своё движение раньше; в) с какой скоростью двигалась каждая машина; г) какая машина прибыла в город В раньше?
1) Распределите, кто отвечает на вопросы а), в), а кто — на вопросы б), г), и ответьте на них. 2) Проверьте друг у друга правильность ответов на поставленные вопросы. 3) Обсудите, что означает точка пересечения графиков. Упражнения для повторения 336. Решите уравнение: а) 3(0,9х - 1) - (х + 0,6) = -0,2; б) 7 - (3,1 - 0,1y) = -0,2y. 338. Запишите в виде выражения сумму трёх последовательных натуральных чисел, меньшее из которых равно: а) n; б) n - 1; в) n + 4. Упростите записанное выражение. Контрольные вопросы и задания 1. Сформулируйте определение прямой пропорциональности. 2. Что является г рафиком прямой пропорциональности? Как построить график прямой пропорциональности? 3. Как расположен в координатной плоскости график функции у = kх при k > 0 и при k < 0? 4. Дайте определение линейной функции. 5. Что является графиком линейной функции? Как построить график линейной функции? 6. В каком случае графики двух линейных функций пересекаются и в каком случае они являются параллельными прямыми? 7. В каких координатных четвертях расположен график функции: у = 6x; у = 0,5х + 4 , у = 3х - 1; у = -3?
|
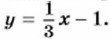Укажите его.
|
|