|
|
|
|
Главная >> Решенния упражнений к учебнику Макарычева. Алгебра 7 класс |
|
|
Домашние работы Линейная функция и её график (окончание)323. у = 0 — если график пересекает ось х. а) у = 0,4х - 12; у = 0 ⇒ 0 = 0,4х — 12 ⇒ 0,4х = 12 ⇒ х = 30 — график пересекает ось х в точке (30; 0); б) у = 324. Чтобы проверить принадлежит точка графику функции или нет, необходимо в уравнение функции подставить координаты данной точки, если получится верное равенство, то точка принадлежит графику у = 1,2х - 7. а) A(100; 113); 1,2х - 7 = 1,2 • 100 - 7 = 120 - 7 = 113 = у — график проходит через точку A; б) B(-15; -25); 1,2х - 7 = 1,2 • (-15) - 7 = -18 - 7 = = -25 = у — график проходит через точку В; в) С(—10; 5); 1,2х - 7 = 1,2 • (-10) - 7 = -12 - 7 = -19 ≠ у — график не проходит через точку С; г) D(300; 353); 1,2х - 7 = 1,2 • 300 - 7 = 360 - 7 = 353 = у — график проходит через точку D.
328. График проходит через точки (5; 2) и (4;3). В уравнение функции подставить координаты данных точек, если получится верное равенство, значит это и есть искомая функция. Эта функция — 4. у = -x + 7.
330. а) Масса пустого бидона равна 1 кг. б) Масса бидона с одним литром жидкости равна 2 кг. в) Для того чтобы найти массу одного литра жидкости необходимо от массы бидона с одним литром жидкости вычесть массу пустого бидона: 2 - 1 = 1 кг. г) 2 литра. 331. а) 6 л; б) 4 мин; в) 6 мин. 332. а) Дачник ехал по шоссе на протяжении 30 минут, за это время он проехал 40 км (30 мин = 0,5 ч),
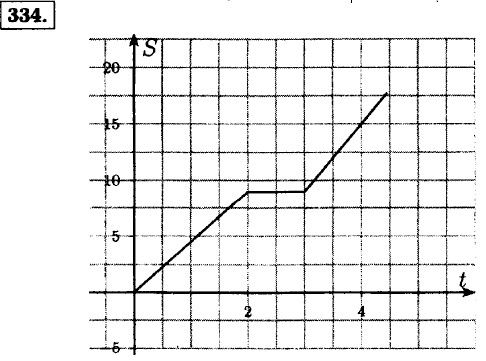
в) За 1 час 10 минут дачник проехал весь путь.
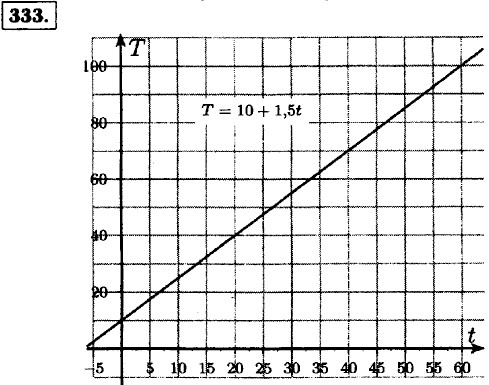
а) 17,5°С, 25°С; б) через 50 мин.
335. а) Первая машина была в пути 2 ч 50 мин, а вторая 1 ч 25 мин. б) Первая машина начала своё движение раньше, в) Вторая машина двигалась со скоростью: 336. а) 3 • (0,9х - 1) - (х + 0,6) = -0,2 ⇒ 2,7х - 3 - х - 0,6 = -0,2 ⇒ 1,7х = 3,4 ⇒ х = 2. б) 7 - (3,1 - 0,1 у) = -0,2y) ⇒ 7 - 3,1 + 0,1 у = -0,2у ⇒ 0,3у = -3,9 ⇒ у = -13. 337. Пусть первая бригада изготовила х деталей, тогда вторая х + 10, а третья 0,3 • (х + х + 10) = 0,3 × (2x + 10). Значит х + х + 10 + 0,3 • (2x + 10) = 65 ⇒ 2x + 10 + 0,6x + 3 = 65 ⇒ 2,6x = 52 ⇒ х = 20, х + 10 = 30, 0,3 • (2x + 10) = 0,3 • (50) = 15. Ответ: первая бригада изготовила 20 деталей, вторая 30, третья 15. 338. а) n + (n + 1) + (n + 2) = 3n + 3; б) (n - 1) + n + (n + 1) = 3n; в) (n + 4) + (n + 5) + (n + 6) = 3n + 15.
|
|
|



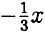 + 8; у = 0 ⇒ =
+ 8; у = 0 ⇒ = 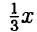 = 8 ⇒ х = 24 — график пересекает ось х в точке (24; 0).
= 8 ⇒ х = 24 — график пересекает ось х в точке (24; 0).
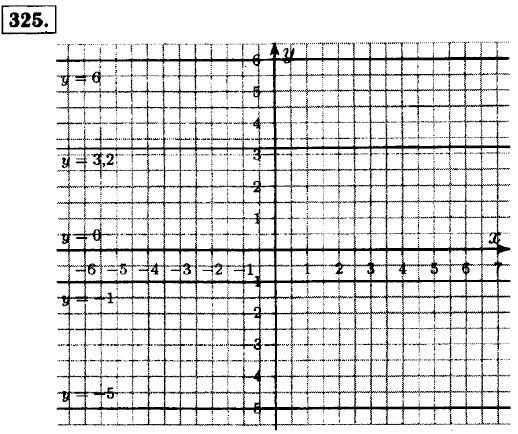
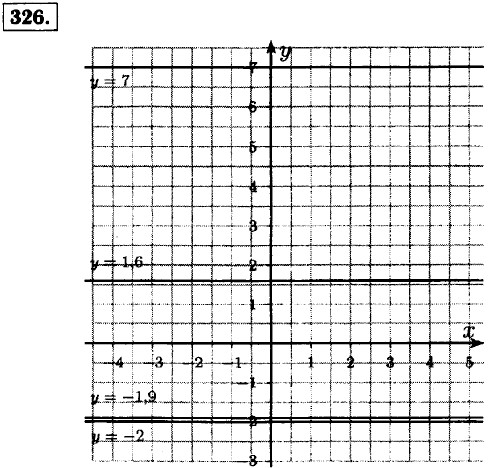

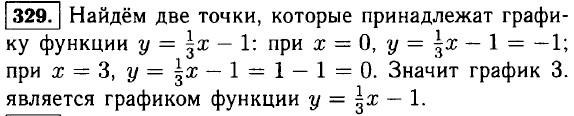
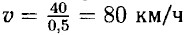 — скорость автомобиля по шоссе.
— скорость автомобиля по шоссе.

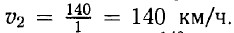 Первая машина двигалась со скоростью:
Первая машина двигалась со скоростью: 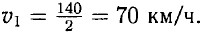 г) Вторая машина прибыла раньше.
г) Вторая машина прибыла раньше.