Линейная функция и её график

Рассмотрим примеры функций.

Пример 1. На шоссе расположены пункты A и В, удаленные друг от друга на 20 км (рис. 29). Мотоциклист выехал из пункта В в направлении, противоположном А, со скоростью 50 км/ч. За t ч мотоциклист проедет 50t км и будет находиться от А на расстоянии 50t + 20 км. Если обозначить буквой s расстояние (в километрах) мотоциклиста до пункта A, то зависимость этого расстояния от времени движения можно выразить формулой

s = 50t + 20,

где t ≥ 0.

Пример 2. Ученик купил тетради но 3 р. за штуку и ручку за 5 р. Обозначим число купленных тетрадей буквой х, а стоимость покупки (в рублях) буквой у. Получим

у = 3х + 5,

где х — натуральное число.

В обоих примерах мы встретились с функциями, заданными формулами вида

y = kx + b,

где х — независимая переменная, k и b — числа.

Такие функции называют линейными функциями.

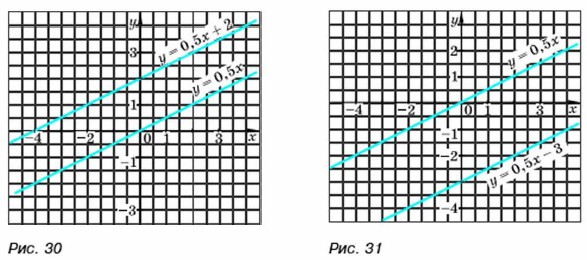
Определение. Линейной функцией называется функция, которую можно задать формулой вида у = kх + b, где х — независимая переменная, k и b — некоторые числа.

Прямая пропорциональность является частным случаем линейной функции. Действительно, при b = 0 формула у = kх + b принимает вид у = kх, а этой формулой при k ≠ 0 задаётся прямая пропорциональность.

Выясним, какой вид имеет график линейной функции.

Рассмотрим, например, функцию у= 0,5х + 2. Сравним значения функций

у = 0,5х + 2 и у = 0,5х

при одних и тех же значениях х.

Из приведённой таблицы и формул у = 0,5х и у= 0,5х + 2 ясно, что для любого значения аргумента х значение функции у = 0,5х + 2 на 2 единицы больше значения функции у = 0,5х. Бели график функции у = 0,5х сдвинуть на 2 единицы вверх (т. е. в направлении оси у), то каждая точка (х₀; у₀) графика функции у = 0,5х перейдёт в точку (х₀; y₀ + 2) графика функции у = 0,5х + 2. При этом любая точка графика функции у = 0,5х + 2 получается из соответствующей точки графика функции у = 0,5х.

Следовательно, график функции у = 0,5х + 2 есть прямая, параллельная графику функции у = 0,5х, проходящая через точку (0; 2) (рис. 30).

Аналогично можно показать, что графиком функции у = 0,5х - 3 является прямая, параллельная прямой у = 0,5х и проходящая через точку (0; -3) (рис. 31). Вообще

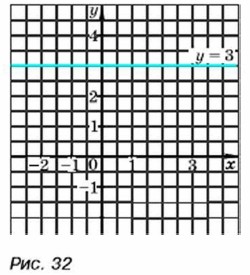
график функции у = kx + b, где k ≠ 0, ость прямая, параллельная прямой у = kх.

Формула у = kх + b при k = 0 принимает вид у = b. В этом случае графиком функции у = kх + b является прямая, параллельная оси х при b ≠ 0 или сама ось х при b = 0.

На рисунке 32 построен график функции у = 3.

Таким образом,

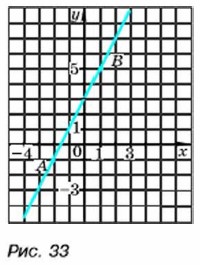
графиком линейной функции является прямая.

Для построения графика линейной функции достаточно найти координаты двух точек графика, отметить эти точки на координатной плоскости и провести через них прямую.

Пример 3. Построим график функции у = 2х + 3.

Функция у = 2х + 3 линейная, поэтому её графиком является прямая. Используя формулу у = 2х + 3, найдём координаты двух точек графика:

если х = -2, то у = 2 • (-2) + 3 = -1;

если х = 1, то у = 2 • 1 + 3 = 5.

Отметим точки А (-2; -1) и В(1; 5). Проведём через эти точки прямую (рис. 33). Прямая АB есть график функции у = 2х + 3.

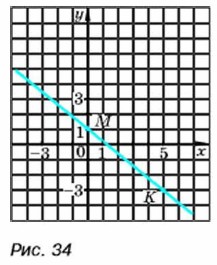
При построении графика линейной функции часто бывает удобно в качестве одной из точек брать точку с абсциссой 0.

Пример 4. Построим график функции у = -0,8x + 1.

Найдём координаты двух точек графика:

если х = 0, то у = -0,8 • 0 + 1 = 1;

если х = 5, то у = -0,8 • 5 + 1 = -3.

Отметим точки М(0; 1) и К(5; -3) и проведём через них прямую (рис. 34). Прямая МК — график функции у = -0,8x + 1.

Продолжение >>>