|
|
|
|
Главная >> Домашние работы к учебнику Макарычева. Алгебра 7 класс |
|
|
Решенния упражнений Дополнительные упражнения к параграфу 6
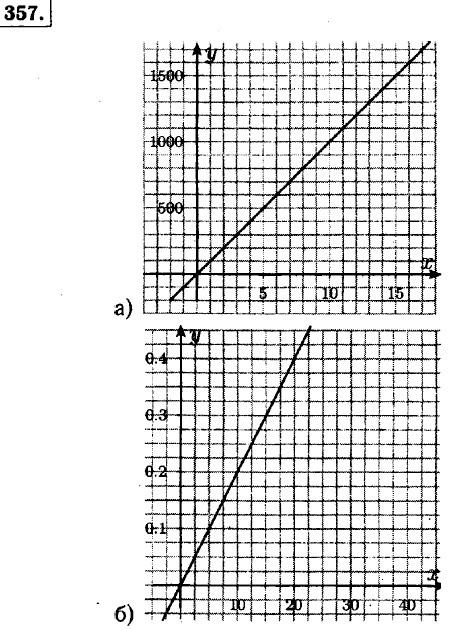
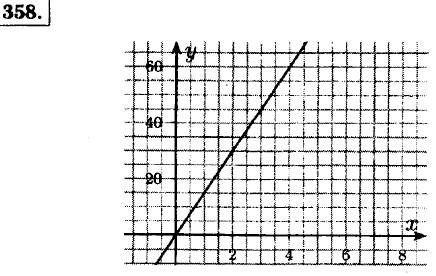
а) если х = 3 ч, то у = 45 км; если х = 3 ч 40 мин, то у = 55 км; б) если у = 50 км, то х ≈ 3,5 ч. 359. 360. у = 0,2х - 4 ⇒ 0,2х = у + 4 ⇒ х = 5у + 20: х = -25 ⇒ у = 0,2 • (-25) - 4 = -5 - 4 = -9; х = -12 ⇒ у = 0,2 • (-12) - 4 = -2,4 - 4 = -6,4; х = 45 ⇒ y = 0,2 • 45 - 4 = 9 - 4 = 5; x = 60 ⇒ у = 0,2 • 60 - 4 = 12 - 4 = 8; у = 0 ⇒ x - 5 • 0 + 20 = 20; у = 1 ⇒ x = 5 • 1 + 20 - 25. а) у = х ⇒ х = 0,2х - 4 ⇒ 0,8х = -4 ⇒ х -5. Да, х = у = -5. б) у = -х, и х = -у ⇒ -х = 0,2х - 4 ⇒ 1,2х = 4 ⇒ х = 361. Зависимость является линейной, значит функцию можно задать формулой вида у = kх + b. а) Известны две точки (0; -8) и (2; 12). Значит -8 = k • 0 + b ⇒ b = -8, 12 = k ⇒ 2 + b ⇒12 = 2k - 8 ⇒ 2k = 20 ⇒ k = 10. Уравнение прямой у - 10х - 8: при х = -2 ⇒ у = -2 • (10) - 8 = -28; при х = 4 ⇒ у = 10 • 4 - 8 = 32; при х = 6 ⇒ у = 10 • 6 - 8 = 52.
б) Известны две точки (0; 5) и (10; 6). Значит 5 = k × 0 + b ⇒ b = 5, 6 = к • 10 + b ⇒ 6 = 10k + 5 ⇒ 10k = 1 ⇒ k = 0,1. Уравнение прямой у = 0,1х + 5: при у = -15 ⇒ -15 = 0,1х + 5 ⇒ 0,1х = -20 ⇒ х = -200; при х = -10 ⇒ у = 0,1 • (-10) + 5 = -1 + 5 = 4; при х = 30 ⇒ у = 0,1 • 30 + 5 = 3 + 5 = 8; при у = 15 ⇒ 15 = 0,1х + 5 ⇒ 0,1х - 10 ⇒ х - 100.
362. Зависимость является линейной, значит функцию можно задать формулой вида у = кх + b. Возмём две точки: (1; 11)11 = 1 • k + 6 и (2; 21)21 = -2 • k + b. Умножим обе части равенства 11 = k + 6 на 2. Получим, 22 = 2k + 2b. Вычтем из 22 = 2k + 2b равенство 21 = 2к + 6, таким образом: 22 - 21 = (2k + 2b) - (2k + b) ⇒ 1 = 2k - 2k + 2k - k ⇒ k = 1, 11 = k + b ⇒ k + 1 = 11 ⇒ k = 10. Формула данной функции: у = 10х + 1. <<< К началу Решенния (окончание) >>>
|
|
|



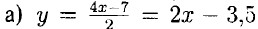 — является линейной функцией; б) у — 3 • (х + 8) = 3x + 24 — является линейной функцией; в) у = х • (6 - х) = 6х - х2 — не является линейной функцией; г) у = х • (9 - х) + х2 = 9х - х2 + х2 = 9х — является линейной функцией.
— является линейной функцией; б) у — 3 • (х + 8) = 3x + 24 — является линейной функцией; в) у = х • (6 - х) = 6х - х2 — не является линейной функцией; г) у = х • (9 - х) + х2 = 9х - х2 + х2 = 9х — является линейной функцией.
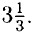 Да, х = -у =
Да, х = -у = 
