|
|
|
|
Главная >> Решенния упражнений к учебнику Макарычева. Алгебра 7 класс |
|
|
Домашние работы Определение степени с натуральным показателем (окончание)
390. Площадь кольца S = πR2 - πr2 = π (R2 - r2) = π (б,42 - 3,62) = π (40,96 - 12,96) = 3,14 • 28 = 87,92 см2. Ответ: 87,92 см2. 391. а) 0,01y4: при у = -2 ⇒ 0,01у4 = 0,01 • (-2)4 = 0,01 • 16 = 0,16; при у = 2 ⇒ 0,01у4 = 0,01 • (2)4 = - 0,01 • 16 = 0,16; при у = -3 ⇒ 0,01y4 = 0,01 × (-3)4 = 0,01 • 81 = 0,81; при у = 3 ⇒ 0,01y4 = 0,01 • (3)4 = 0,01 • 81 = 0,81; при у = -10 ⇒ 0,01 у4 = 0,01 • (-10)4 = 0,01 • 10000 = 100; при у = 10 ⇒ 0,01у4 = 0,01 • (10)4 = 0,01 • 10000 = 100. б) 2с2 + 3; при с = -11 ⇒ 2с2 + 3 = 2 • (-11)2 + 3 = 2 • 121 + 3 = 242 + 3 = 245; при с = 11 ⇒ 2с2 + 3 = 2 • (11)2 + 3 = 2 • 121 + 3 = 242 + 3 = 245; при с = 0 ⇒ 2с2 + 3 = 2 • (0)2 + 3 = 20 + 3 = 0 + 3 = 3; при с = -15 ⇒ 2с2 + 3 = 2 • (-15)2 + 3 = 2 • 225 + 3 = 450 + 3 = 453; при с = 15 ⇒ 2с2 + 3 = 2 • (15)2 + 3 = 2 • 225 + 3 = 450 + 3 = 453. 392.а) х2 = (-х)2 — так как степень чётная: при х = -9 ⇒ х2 = (-x)2 = 81 ⇒ -х2 = -81; при х = 9 ⇒ х2 = (-х)2 = 81 ⇒ -х2 = -81; при x = -6 ⇒ х2 = (-х)2 = 36 ⇒ -х2 = -36; при x = 6 ⇒ x2 = (-x)2 = 36 ⇒ -х2 = -36; при х = -2 ⇒ x2 = (-х)2 = 4 ⇒ -х2 = -4; при х = 2 ⇒ x2 =(-х)2 = 4 ⇒ -х2 = -4. б) -х3 = (-х)3 — так как степень не чётная: при х = -4 ⇒ -х3 = (-х)3 = 64 ⇒ х3 = -64; при x = 4 ⇒ -х3 = (-х)3 = -64 ⇒ х3 = 64; при x = -3 ⇒ -х3 = (-x)3 = 27 ⇒ х3 = -27; при x = 3 ⇒ -х3 = (-х)3 = -27 ⇒ х3 = 27; при х = -1 ⇒ -х3 = (-х)3 = 1 ⇒ х3 = -1; при х = 1 ⇒ -x3 = (- х)3 = -1 ⇒ х3 = 1 393. x5 + x4 + х3 + х2 + х: при х = -1 ⇒ x5 + x4 + x3 + х2 + х = -1 + 1 - 1 + 1 - 1 = -1; при x = 0 ⇒ x5 + x4 + x3 + x2 + x = 0; при х = 10 ⇒ x5 + x4 + x3 + х2 + х = 100000 + 10000 + 1000 + 100 + 10 = 111110. 394. 1) 90 = 2 • 3 • 3 • 5, 15 = 3 • 5. 2) В разложение числа а должны входить множители 2 и 32. 3) а = 2 • 32 = 18 или а = 2 • З2 • 5 = 90 395. а) а3а = а4; б) а4а2 = а6; в) а3а6 = а9; г) а20а12 = а32. 396. 4x2 ≥ 0 и (х - 8)2 ≥ 0, так как при возведении любого числа в чётную степень результат не отрицательный. 397. а) а2 + 1; 3 + (5 - а)2; а4 + а2 + 8; б) -а6 -4а4 - 1; -а8 - 9. 398. а) (х + 1)2; б) а2 + b2; в) m2 - n2; г) (b - n)2; д) 2 • х2 • у2; е) 2 • а3 • b2. 399. а) квадрат суммы чисел x и у; б) сумма квадратов чисел ж и у; в) квадрат разность чисел x и у; г) разность квадратов чисел x и у; д) куб разности чисел x и у; е) сумма кубов чисел x и у; ж) удвоенный квадрат разность чисел а и b; з) утроенная сумма квадратов чисел а и b. 400. у = 1,2x - 30: график пересекает ось ж при у = 0. Значит 0 = 1,2x = 30 ⇒ 1,2x = 30 ⇒ x = 25; график пересекает ось у при x = 0. Значит у = 1,2 • 0 - 30 = -30. График функции у = 1,2x - 30 пересекает ось ж в точке (25; 0), и ось у в точке (0; -30). 401. а) у = -4x + 1,3 и у = x - 2,7, значит -4x + 1,3 = x - 2,7 ⇒ 5x = 4 ⇒ x = 0,8; у = -4x + 1,3 = -4 • 0,8 + 1,3 = -1,9. Точка пересечения: (0,8; -1,9). б) у = -x + 8,1 и у = -3x + 7,9, значит -x + 8,1 = -3x + 7,9 ⇒ 2x = -0,2 ⇒ x = -0,1 ⇒ у = -x + 8,1 = 0,1 + 8,1 = 8,2. Точка пересечения: (-0,1; 8,2). 402. а) Графики параллельны, так как у них равны угловые коэффициенты k. Причём, график у = б) Графики не параллельны, так как у них не равны угловые коэффициенты k. Значит у них есть точка пересечения. Эта точка (0;4).
|
|
|



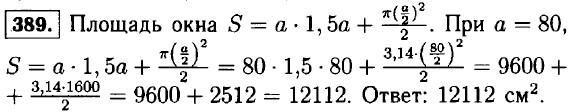
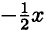 + 3 — выше относительно оси ж, чем график у =
+ 3 — выше относительно оси ж, чем график у = 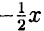 - 3.
- 3.