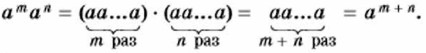Умножение и деление степеней

Выражение а²а³ представляет собой произведение двух степеней с одинаковыми основаниями. Это произведение можно записать в виде степени с тем же основанием:

а²а³ = (аа) • (ааа) = ааааа = а⁵.

Значит,

а²а³ = а^{2 + 3}.

Мы видим, что произведение а²а³ равно степени с тем же основанием и показателем, равным сумме показателей перемножаемых степеней. Аналогичным свойством обладает произведение любых степеней с одинаковыми основаниями.

Для любого числа а и произвольных натуральных чисел m и n

а^mаⁿ = а^{m + n}.

Для доказательства используем определение степени и свойства умножения. Представим выражение атая сначала в виде произведения множителей, каждый из которых равен а, а затем в виде степени

Таким образом,

а^mаⁿ = а^{m + n}.

Доказанное равенство выражает основное свойство степени. Оно распространяется на произведение трех и более степеней. Например:

а^mаⁿа^k = а^{m + n}а^k = а^{(m + n) + k} = а^{m + n + k}.

Из основного свойства степени следует правило умножения степеней:

при умножении степеней с одинаковыми основаниями основание оставляют прежним, а показатели степеней складывают.

Приведём примеры:

Х²Х⁷ = x^{8 + 7} = x¹⁵, yy⁵ = y¹y⁵ = y^{1 + 5} = y6, b²b⁴b² = b^{2 + 4 + 3} = b⁹.

Выражение a⁷ : а² является частным двух степеней с одинаковыми основаниями. Оно имеет смысл при а ≠ 0. Если а ≠ 0, то это частное можно представить в виде степени с тем же основанием. Действительно, так как а² • а⁴ = а⁷, то по определению частного

а⁷ : а² = а⁴, т. е. а⁷ : а² = а^{7 - 2}.

Мы видим, что частное а⁷ : а³ при а ≠ 0 равно степени с тем же основанием и показателем, равным разности показателей делимого и делителя.

Аналогичным свойством обладает любое частное степеней с одинаковыми основаниями, отличными от нуля, в котором показатель степени делимого больше показателя степени делителя.

Для любого числа а ≠ 0 и произвольных натуральных чисел тип, таких, что m > n,

а^m : аⁿ = а^{m - n}.

Равенство а^m : аⁿ = а^{m - n} будет доказано, если мы установим, что произведение а^{m - n} и аⁿ равно а^m.

Применив к произведению а^{m - n}аⁿ основное свойство степени, получим

а^{m - n}аⁿ = a(m - n) + n = am - n + n = a^m.

Значит, по определению частного а^m : аⁿ = а^{m - n}.

Продолжение >>>