Функции у = х₂ и у = х₃ и их графики

Зависимость площади квадрата от его стороны и зависимость объёма куба от его ребра являются примерами функций, которые задаются формулами вида у = х² и у = x³.

Построим график функции у = х². Составим таблицу соответственных значений х и у:

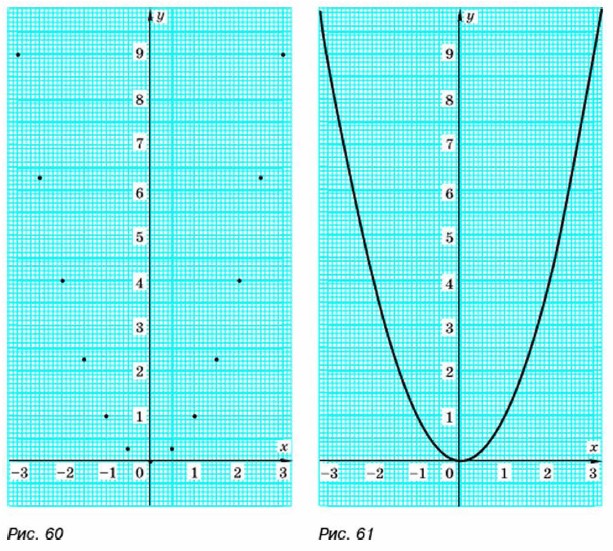
Построим точки, координаты которых указаны в таблице (рис. 60). Чтобы точнее построить график вблизи начала координат, вычислим ещё несколько значений функции:

Из таблицы видно, что при значениях х близких к нулю значения функции мало отличаются от нуля. Значит, график функции вблизи начала координат почти сливается с осью х.

Через отмеченные точки проведём плавную линию (рис. 61). Получим график функции у = х².

Ясно, что график функции у = х² неограниченно продолжается вверх справа и слева от оси у.

График функции у = х² называют параболой.

Выясним некоторые свойства функции у = х².

1. Если х = 0, то у = 0. Поэтому график функции проходит через начало координат.
2. Если х ≠ 0, то у > 0. Действительно, квадрат любого числа, отличного от нуля, положителен. Значит, все точки графика функции, кроме точки (0; 0), расположены выше оси х.
3. Противоположным значениям х соответствует одно и то же значение у. Это следует из того, что (-х)² = х² при любом х. «Значит, точки графика, имеющие противоположные абсциссы, симметричны относительно оси у.

Построим теперь график функции у = х3. Составим таблицу соответственных значений х и у, округляя значение у до сотых:

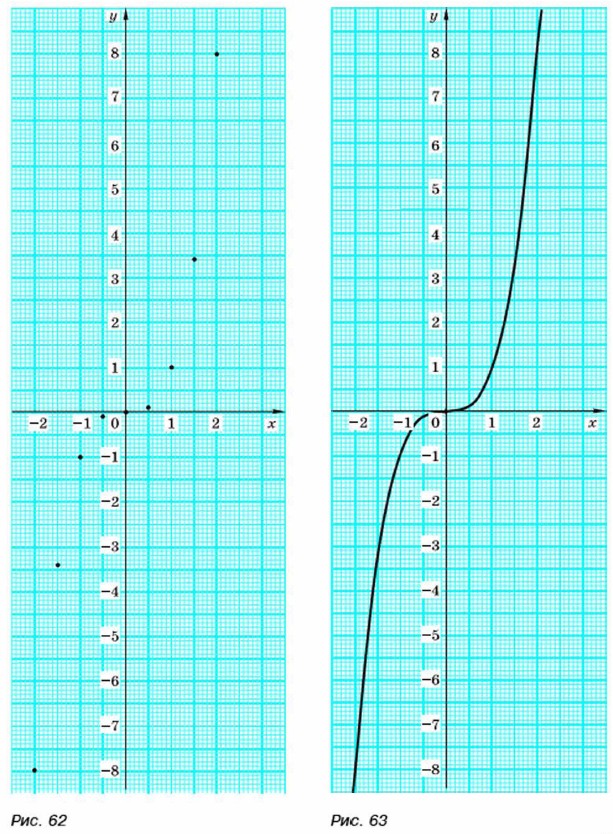
Построим точки, координаты которых указаны в таблице (рис. 62).

Через отмеченные точки проведём плавную линию (рис. 63). Получим график функции у = х³. Ясно, что этот график неограниченно продолжается справа от оси у вверх и слева от оси у вниз.

Заметим, что вблизи начала координат график функции почти сливается с осью х (если х = 0,2, то у = 0,008; если х = 0,3, то у = 0,027).

Продолжение >>>

Функции у = х2 и у = х3 и их графики

Функции у = х₂ и у = х₃ и их графики