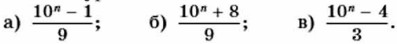|
|
|
|
|
Дополнительные упражнения к главе 3 К параграфу 7511. Верно ли равенство: а) 32 + 42 + 52 = 62; б) (1 + 2 + 3 + 4)2 = 13 + 23 + 33 + 43? 512. Докажите, что 267 + 155 - 119 кратно 10. 513. Разложив число на простые множители, представьте ого в виде произведения степеней простых чисел: а) 54; б) 144; в) 225; г) 500. 514. Представьте число в виде степени с основанием 2 или 3: а) 64; б) 81; в) 512; г) 729; д) 1024. 515. Представьте число в виде суммы степеней числа 2: а) 6; б) 18; в) 42. 516. Представьте число в виде степени с показателем, отличным от 1: а) 121; б) -32; в) 0,125; г) 625; д) -0,216; е) 0,343. 517. Найдите значение выражения:
518. Найдите значение выражения (—1 )n при n, равном: а) 6; б) 11; в) 23; г) 70. 519. Вычислите: а) сумму кубов чисел 5 и -3; б) куб суммы чисел 9 и -11; в) разность квадратов чисел 12 и 8; г) квадрат разности чисел 96 и -4; д) удвоенное произведение квадратов чисел 7 и -5; е) утроенное произведение числа 15 и квадрата числа 4. 520. Не выполняя вычислений, сравните значения выражений:
521. Что больше и на сколько:
522. Сравните значения выражений а2 и а3 при а, равном: а) -12; б) 0; в) 5. 523. Найдите при х = 1,5 и х = -2 значения выражений: а) х2, -х2, (-х)2; б) х3, -х3, (—х)3. 524. Докажите, что при любом натуральном п значение дроби является натуральным числом:
525. Какие из чисел -3, -2, -1, 1, 2, 3 являются корнями уравнения:
526. Докажите, что не имеет корней уравнение: а) х2 + 1 = 0; б) 2х6 + 3х4 + х2 + 1 = 0. 527. При каком значении х значение выражения (2х + 3)2 равно нулю? 528. Докажите, что уравнение х4 + 3х3 + 2х2 + х + 6 = 0 не имеет положительных корней. 529. Имеет ли уравнение х6 - х5 + х4 - х3 + х2 - х +1 = 0 отрицательные корни?
|
|
|