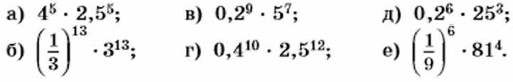|
|
|
|
|
Дополнительные упражнения к главе 3 К параграфу 7 (окончание)530. Упростите выражение: а) а10а12(-а5); б) х(-х)(-х6); в) yky8y2; г) bnbnb3. 531. Представьте выражение в виде степени: a) 25 • 8; б) 16 • 64; в) 7n • 343; г) 81 • 3k. 532. Представьте выражение в виде произведения двух множителей, один из которых равен а5; а) а10; б) а6; в) -а40. 533. Замените х степенью с основанием с так, чтобы полученное равенство было тождеством: а) с2х = с5; б) xc5 = с9; в) с6х = с11; г) с4х = с15. 534. Замените частное степенью: а) b15 : b12; б) 739 : 713; в) а11 : а; г) 12100 : 1299. 535. Найдите значение выражения:
536. Упростите выражение: а) 6n + 3 : 6n; б) 10n + 1 : 10n - 1. 537. Вычислите:
538. Упростите: а) (-1)n • (-1)n; б) (-1)2n : (-1)3. S39. Площадь круга вычисляется по формуле S = πr2, где r — радиус круга. Как изменится площадь круга, если его радиус увеличить в 3 раза? в 7 раз? 540. Объём шара вычисляется по формуле 541. Верно ли при любом значении х равенство: а) |х|2 = х2; б) |х|3 = х3? 542. Найдите значение выражения:
543. Сравните значения выражений:
544. Представьте выражение в виде 3n или - 3n: а) (-33)2; б) (-32)3; в) -(34)2; г) -(-32)3. 545. Упростите выражение:
546. Замените букву р выражением так, чтобы полученное равенство было тождеством: а) р5 = х20; б) р7 = х21; в) р2с8 = с20; г) у7 • (у2)4 = p5. 547. Представьте в виде степени: а) 45 • 221; б) 2513 : 511; в) 85 • 1613; г) 2710 : 915. 548. Представьте выражение в виде хn или -хn: а) (-х3)7; б) (-х2)5; в) (-х)4х8; г) (-х5)7 • (х2)3. 549. Сколькими способами можно представить в виде степени с показателем, отличным от 1, число: а) 215; б) 26? 550. При каком условии: а) сумма квадратов двух чисел равна нулю; б) квадрат суммы двух чисел равен нулю? 551. Натуральное число а оканчивается единицей. Какой цифрой оканчивается степень числа а с натуральным показателем? Для каких ещё цифр выполняется аналогичное свойство? 552. Докажите, что при любом натуральном k: а) число 34k оканчивается единицей; б) число 10k - 1 кратно 3.
|
|
|



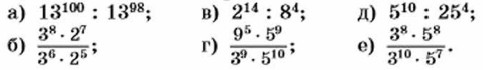
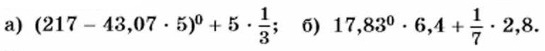
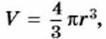 где r — радиус шара. Как изменится объём шара, если радиус увеличить в 2 раза? в 4 раза?
где r — радиус шара. Как изменится объём шара, если радиус увеличить в 2 раза? в 4 раза?