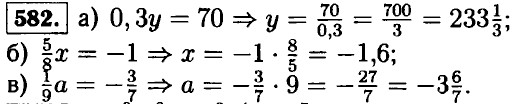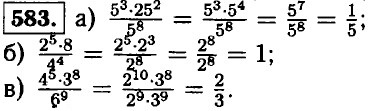Многочлен и его стандартный вид

567. а) Членами многочлена -6x⁴ + y³ - 5у + 11 являются одночлены -6x⁴; у³; -5у; 11; б) Членами многочлена 25аb + аb² - а²b + 8а - 7b являются одночлены 25аb; аb²; -а²b; 8а; -7b.

568. а) 10x - 8ху - 3ху = 10х + (-8ху - 3ху) = 10x -11ху,

б) 2аb - 7аb + 7а² = (2аb - 7аb) + 7а² = -5аb + 7а²;

в) 3x⁴ - 5x + 7х² - 8x⁴ + 5x = (3x⁴ - 8x⁴) + (-5x + + 5х) + 7х² = -5x⁴ + 7x²;

г) 2а³ + а² - 17 - 3а² + а³ - а - 80 = (2а³ + а³) + (а² - 3а²) + (-17 - 80) - а = 3а³ -2а² - а - 97.

569. 1. 4а² - 4b - а² + 17b - b = 3а² + 12b;

2. -0,7а² - 7b - 2,3а² + 8b = -3а² + b;

3. 12а² - 9b - 9а² + 6b + b = 3а² - 2b;

4. 1,8а² - 4,2b + 1,2а² + 5b + 0,2b = 3а² + b.

Многочлен 4. тождественно равен выражению 3а² + 6.

570. а) -8р⁴ + 12р³ + 4р⁴ - 8р² + 3р² = -4р⁴ + 12р³ - 5р²;

б) 2аа² + а2 - 3а² + а³ - а = (2а³ + а³) + (а² - 3а²) - а = 3а³ - 2а² - а;

в) 3xx⁴ + 3xx³ - 5х²х³ - 5x²x = (3x⁵ - 5x⁵) + 3x⁴ - 5x³ = -2x5 + 3x⁴ - 5x³;

г) 3а • 4b² - 0,8b • 4b² - 2аb • 3b + b • 3b² - 1 = 12аb² - 3,2b³ - 6аb² + 3b³ - 1 = 6аb² - 0,26³ - 1.

571. а) 2а²x³ - ах³ - а⁴ - а²х³ + ах³ + 2а⁴ = (2а²x³ - а²х³) + (-ах³ + ах3) + (-а⁴ + 2а⁴) = а²х³ + а⁴;

б) 5x • 2у² - 5х • 3ху — х²у + 6xy² = (10xу² + 6ху²) + (-15х²у - х²у) = 16xу² - 16х²у.

572. а) 5х⁶ - 3х² + 7 - 2х⁶ - 3х⁶ + 4х² = (5х⁶ - 2х⁶ - 3х⁶) + (-3х² + 4х²) + 7 = х² + 7: при х = -10 ⇒ х² + 7 = (-10)² + 7 = 107;

б) 4а²b — ab² - 3a²b + ab² - ab + 6 = (4а²b - 3а²b) + (-a^b2 + ab²) - ab + 6 = a²b - ab + 6: при а = -3, b = 2 ⇒ a²b - ab + 6 = (-3)² • 2 - (-3 • 2) + 6 = 18 + 6 + 6 = 30.

573. а) 6а³ - а¹⁰ + 4а³ + а¹⁰ - 8а³ + а = (-а¹⁰ + а¹⁰) + (6а³ + 4а³ - 8а³) + а = 2а³ + а: при а = -3 ⇒ 2а³ + а = 2 • (-3)³ - 3 = -54 - 3 = -57;

б) 4х⁶у³ - 3х⁶у³ + 2х²у² - х⁶у³ - х²у² + у = (4х⁶у³ - 3х⁶у³ - х⁶у³) + (2х²у² - х²у²) + у = х²у² + у: при х = -2, у = -1 ⇒ х²у² + у = (-2)² • (-1)² -1 = 4 -1= 3.

574. 2х² + 1: при х = 0 ⇒ 2х² + 1 = 2 • 0² + 1 = 1; при х = -2 ⇒ 2х² + 1 = 2 • (-2)² + 1 = 8 + 1 = 9; при х = 3 ⇒ 2х² + 1 = 2 • 3² + 1 = 18 + 1 = 19; при х = -4 ⇒ 2х² + 1 = 2 • (-4)² + 1 = 32 + 1 = 33. Так как 2х² ≥ 0, значит 2х² + 1 ≥ 1 и значение многочлена не при каких х не равно 0 и не отрицательно.

575. х² ≥ 0; у² ≥ 0, значит х² + у² + 1 ≥ 1 при любых значениях х.

576. а) 10а + b; б) 100а + 10b + с.

577. а) 17а⁴ - 8а⁵ + 3а - а³ - 1 = -8а⁵ + 17а⁴ - а3 + 3a - 1; б) 35 - с⁶ + 5с² - с⁴ = -с6^{- с⁴ + 5с² + 35.}

578. а) x⁴ - 5 - х² + 12х = -5 + 12х - х² + х⁴; б) 2y + y³ - y² + 1 = 1 + 2у - у² + у³.

579. Степенью многочлена стандартного вида называют наибольшую из степеней входящих в него одночленов. а) 4а⁶ - 2а⁷ + а - 1 — многочлен седьмой степени; б) 5р³ - р - 2 — многочлен третей степени; в) 1 - 3х — многочлен первой степени; г) 4ху + ху² - 5х² + у — многочлен третей степени; д) 8х⁴у + 5х²у³ - 11 — многочлен пятой степени; е) xy + yz + xz - 1 — многочлен второй степени.

580. а) при x = 1,97; x² + 4,23 = 1,97² + 4,23 = 8,1109; б) при a = 2,3; a⁴ + 2a = 27,9841 + 4,6 = 32,5841.

581. 1) a) 2555 - 2 = 2553 = 37 • 69; 6) 7111 - 7 = 7104 = 37 • 192; в) 8999 - 8 = 8991 = 37 • 243; г) 9666 - 9 = 9657 = 37 • 261.

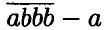2) Разность вида можно представить в виде суммы: 1000а + 100b + 10b + b - а = 999а + 111b = 111 • (9а + b) = 37 • 3 • (9а + b), значит всякая разность вида делится на 37.

584. y = 0,01x ⇒ x 100y; a) при y = 240 ⇒ x = 100 • 240 = 24000; б) при у = -100 ⇒ х = 100 • (-100) = -10000.

<<< К началу