|
|
|
|
|
§ 9. Сумма и разность многочленов Сложение и вычитание многочленов (окончание)605. Решите уравнение: а) (23 + 3х) + (8х - 41) = 15; б) (19 + 2х) - (5х -11) = 25; в) (3,2у - 1,8) - (5,2у + 3,4) = -5,8; г) 1 - (0,5х - 15,8) = 12,8 - 0,7х; д) 3,8 - 1,5у + (4,5у - 0,8) = 2,4y + 3; е) 4,2у + 0,8 = 6,2у - (1,1у + 0,8) + 1,2. 606. Решите уравнение: а) 8y - 3 - (5 - 2у) = 4,3; б) 0,5у - 1 - (2у + 4) = у; в) -8х + (4 + 3х) = 10 - х; г) 1,3х - 2 - (3,3х + 5) = 2х + 1. 607. Представьте выражение в виде суммы каких-нибудь двучленов: а) 3х3 - 2х2 - х + 4; б) -5у4 + 4у3 + 3у2 - 2у. 608. Представьте выражение каким-либо способом в виде разности одночлена и трёхчлена: а) х3 + 2х2 - 3х - 5; б) 3а4 + 2а3 + 5а2 - 4. 609. Известно, что при некоторых натуральных значениях п значение выражения n3 + n кратно 30. Будет ли кратно 30 при тех же значениях п значение выражения: а) n3 + 31n; б) n3 - 29n? 610. (Для работы в парах.) Докажите, что сумма: а) трёх последовательных натуральных чисел кратна 3; б) четырёх последовательных натуральных чисел не кратна 4. 1) Распределите, кто выполняет задание а), а кто — задание б), и выполните их. 2) Проверьте друг у друга правильность выполнения преобразований. 3) Выскажите аналогичное предположение о сумме пяти последовательных натуральных чисел и проверьте, верно ли оно. 611. (Задача исследование.) В «Арифметике» Магницкого, написанной в начале XVIII в., предлагается такой способ угадывания задуманного двузначного числа: «Если кто задумал двузначное число, то скажи ему, чтобы он увеличил число десятков в 2 раза и к произведению прибавил 5 единиц; затем полученную сумму увеличил в 5 раз и к новому произведению прибавил 10 единиц и число единиц задуманного числа, а результат произведённых действий сообщил бы тебе. Если ты из указанного результата вычтешь 35, то узнаешь задуманное число». 1) Выберите двузначное число и проверьте предложенный способ угадывания задуманного числа. 2) Предложите соседу но парте задумать двузначное число, выполнить указанные в условии задачи действия и сообщить результат. 3) Найдите число, задуманное соседом. 4) Докажите справедливость способа отгадывания задуманного двузначного числа, предложенного в учебнике Магницкого. Упражнения для повторения 612. Представьте выражение в виде одночлена:
613. С помощью калькулятора найдите значение выражения х2 - у, если х = 1,4, у = 0,157. Контрольные вопросы и задания 1. Дайте определение многочлена. 2. На примере многочлена 3. Что называется степенью многочлена? Приведите пример многочлена третьей степени. 4. Составьте сумму и разность многочленов х2 - 3у + 6 и -х2 + 3y + 1 и преобразуйте каждое выражение в многочлен стандартного вида. 5. В многочлене 5х2 - х + 4 заключите в скобки два последних члена, поставив перед скобками: а) знак «плюс»; б) знак «минус».
|
|
|



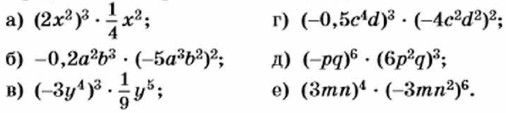
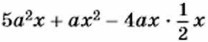 объясните, как привести многочлен к стандартному виду.
объясните, как привести многочлен к стандартному виду.