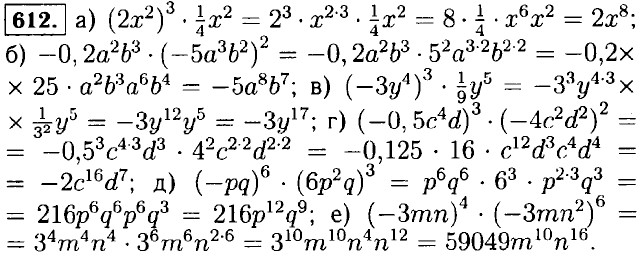|
|
|
|
Главная >> Решенния упражнений к учебнику Макарычева. Алгебра 7 класс |
|
|
Домашние работы Сложение и вычитание многочленов (окончание)598. 5x2 - (3xy - 7x2) + (5xy - 12x2) = 5x2 + 7x2 - 12x2 — 3xy + 5ху = 2xy; а) при x = -0,25 и у = 4 ⇒ 2xy = 2 • (-0,25) • 4 = -2. б) при x = -5 и у = 0,1 ⇒ 2ху = 2 • (-5) • 0,1 = -1. 599. 0,7х4 + 0,2х2 - 5 - (-0,3x4 + 600. 1) Ученик окажется прав, если переменная b сократится. 2) (7а3 - 6b2а + 5аb2) + (5а3 + 7а2b + 3ab2) - (10а3 + a2b + 8ab2) = 7а3 + 5а3 - 10а3 - 6а2b + 7а2b = а2b + 5ab2 + 3ab2 = 8ab2 = 2а3: при а = -0,25 ⇒ 2а3 = 2 • (-0,015625) = -0,03125. 3) Ученик был не прав. 601. х2 + у2 - 2ху + 1: а) у2 +1 - (х2 + у2 - 2xy + 1) = у2 + 1 - х2 - у2 + 2ху - 1 = -х2 + 2ху; б) а2 + 1 - (а2 + у2 - 2ху + 1) = х2 +1 - х2 - у2 + 2ху - 1 = -у2 + 2ху. 602. 603. а) 1,7 - 10b2 - (1 - 3b2) + (2,3 + 7b2) = (-10b2 + 3b2 + 7b2) + (1,7 - 1 + 2,3) = 3 — значение выражения не зависит от значения переменной; б) 1 - b2 - (3b - 2b2) + (1 + 3b - b2) = (-b2 + 2b2 - b2) + (-3b + 3b) + 1 + 1 = 2 — значение выражения не зависит от значения переменной. 604. х = 5а2 + 6ab - b2; у = -4а2 + 2ab + 3b2; z = 9а2 + 4аb: a) х + у + z = 5а2 + 6аb - b2 - 4а2 + 2аb + 3b2 + 9а2 + 4аb = (5а2 - 4а2 + 9а2) + (6аb + 2аb + 4аb) + (-b2 + 3b2) = 10а2 + 12аб + 2б2; б) х — у — z = 5а2 + + баб — б2 — (—4а2 + 2аб + Зб2) — (9а2 + 4аb) = (5а2 + 4а2 - 9а2) + (6аb — 2аb - 4аb) + (-б2 - 3b2) = -4b2. 605. а) (23 + 3x) + (8х - 41) = 15 ⇒ 23 + 3х + 8x - 41 = (3х + 8х) + (23 - 41) = 11х - 18 ⇒ 11х - 18 = 15 ⇒ 11х = 33 ⇒ х = 3; б) (19 + 2х) - (5х - 11) = 25 ⇒ 19 + 2х - 5х + 11 = (2х - 5х) + (19 + 11) = 30 - 3х ⇒ 30 - 3х = 25 ⇒ 3х = 5 ⇒ х = в) (3,2у - 1,8) - (5,2у + 3,4) = -5,8 ⇒ 3,2у - 1,8 - 5,2у - 3,4 = (3,2у - 5,2y) + (-1,8 - 3,4) = -2у - 5,2 ⇒ -2у - 5,2 = -5,8 ⇒ 2у = 0,6 ⇒ у = 0,3; г) 1 - (0,5х - 15,8) = 12,8 - 0, 7х ⇒ 1 - 0,5х + 15,8 = 12,8 - 0,7х ⇒ 0, 7х - 0, 5х = 12,8 - 15,8 - 1 ⇒ 0,2х = -4 ⇒ х = -20; д) 3,8 - 1,5у + (4,5у-0,8) =2,4у + 3 ⇒ 3,8 -1,5у + 4,5у - 0,8 = 2,4у + 3 ⇒ -1,5y + 4,5y - 2,4у = 3 + 0,8 - 3,8 ⇒ 0,6у = 0 ⇒ у = 0; е) 4,2у + 0,8 = 6,2у - (1,1у + 0,8) + 1,2 ⇒ 4,2у + 0,8 = 6,2у - 1,1у - 0,8 + 1,2 ⇒ 4,2у - 6,2у + 1,1у = -0,8 + 1,2 - 0,8 ⇒ -0,9у = -0,4 ⇒ у = 606.) а) 8у - 3 - (5 - 2у) = 4,3 ⇒ 8у - 3 - 5 + 2у = 4,3 ⇒ 8у + 2у = 4,3 + 3 + 5 ⇒ 10у = 12,3 ⇒ у = 1,23 б) 0,5у - 1 - (2у + 4) = у ⇒ 0,5у - 1 - 2у - 4 = у ⇒ 0,5у - 2у - у = 4 + 1 ⇒ -2,5у - 5 ⇒ у = -2 в) -8х + (4 + 3х) = 10 - х ⇒ -8х + 4 + 3х = 10 - х ⇒ -8х + 3х + х = 10 - 4 ⇒ -4х = 6 ⇒ х = -1,5 г) 1,3х - 2 - (3,3х + 5) = 2х + 1 ⇒ 1,3х - 2 - 3, 3х - 5 = 2х + 1 ⇒ 1,3х - 3, 3х - 2х = 1 + 5 + 2 ⇒ -4х = 8 ⇒ х = -2 607. а) 3x3 - 2х2 - х + 4 = (3x3 - х) + (4 - 2x2); б) -5у4 + 4у3 + 3у2 -2у = (4у3 - 5у4) + (3у2 - 2у). 608. а) х3 + 2x2 - 3x - 5 = 2x2 - (3х + 5 - x3); б) 3а4 + 2а3 + 5а2 - 4 = 5а2 - (4 - 3а4 - 2а3). 609. Известно, что выражение n3 + n кратно 30: а) n3 + 31n = n3 + n + 30n; n3 + n и 30n — кратно 30. Значит и значение выражения n3 + 31n будет кратно 30; б) n3 -29n = n3 + п - 30n; n3 + n и 30n — кратно 30. Значит и значение выражения n3 - 29n будет кратно 30. 610. а) Пусть первое число х, тогда второе х + 1, третье х + 2. Их сумма: x + x + 1+ x + 2 = 3x + 3 = 3 • (х + 1) — кратна 3. б) Пусть первое число у, тогда второе у + 1, третье у + 2, четвёртое у + 3. Их сумма: у + у + 1 + у + 2 + у + 3 = 4у + 6.
611. Пусть число десятков а, а единиц b. Увеличим число десятков в 2 раза, получим 2а, затем к произведению прибавим 5, 2а + 5. Полученную сумму увеличим в 5 раз, 5 • (2а + 5) = 10а + 25, к новому произведению прибавим 10 и число единиц, 10а + 25 + 10 + b = 10а + 35 + b. Вычтем из указанного результата 35, 10а + 35 + b — 35 = 10а + b — задуманное число.
613. При x = 1,4 и у = 0,157 ⇒ х2 - у - 1,42 - 0,157 = 1,96 - 0,157= 1,803.
|
|
|



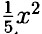 = 8) = 0,7x4 + 0,2x2 - 5 + 0,3x4 - 0,2x2 + 8 = х4 + 3. При любых значениях x4 > 0, значит х4 + 3 > 3.
= 8) = 0,7x4 + 0,2x2 - 5 + 0,3x4 - 0,2x2 + 8 = х4 + 3. При любых значениях x4 > 0, значит х4 + 3 > 3.
 - 0,4xу - 1,5y + 1) - (у2 -
- 0,4xу - 1,5y + 1) - (у2 - 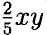 + 0,6x2) = 0,6x2 - 0,4xу - 1,5y + 1 - у2 + 0,4xу - 0,6x2 = (0,6x2 — 0,6x2) + (-0,4xу + 0,4xу) - у2 - 1,5y +1 = -у2 - 1,5у + 1 — значение выражения не зависит
от х.
+ 0,6x2) = 0,6x2 - 0,4xу - 1,5y + 1 - у2 + 0,4xу - 0,6x2 = (0,6x2 — 0,6x2) + (-0,4xу + 0,4xу) - у2 - 1,5y +1 = -у2 - 1,5у + 1 — значение выражения не зависит
от х.
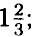
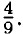
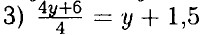 — не целое число, значит сумма четырёх последовательных натуральных чисел не кратна 4.
— не целое число, значит сумма четырёх последовательных натуральных чисел не кратна 4.