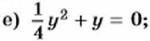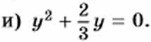Главная >> Алгебра 7 класс. Макарычев. ГДЗ

§ 10. Произведение одночлена и многочлена

Вынесение общего множителя за скобки (продолжение)

Пример 4. Решим уравнение 2х2 + 3х = 0.

В выражении 2х2 + 3х вынесем за скобки множитель х. Получим

    х(2х + 3) = 0.

Произведение х(2х + 3) равно нулю тогда и только тогда, когда равен нулю хотя бы один из множителей, т. е. когда

    х = 0 или 2х + 3 = 0.

Решая уравнение 2х + 3 = 0, находим 2х = -3, х = -1,5.

Следовательно, произведение х(2х + 3) обращается в нуль при х = 0 и при х = -1,5, т. е. уравнение 2х2 + 3х = 0 имеет два корня: 0 и -1,5.

Запись можно вести короче:

    2х2 + 3х = 0,

    х(2х + 3) = 0,

    х = 0 или 2х + 3 = 0,

    х = 0 или х = -1,5.

Ответ: 0 и -1,5.

Пример 5. Докажем, что сумма 39 + 37 + 36 делится на 31.

Вынесем в выражении 39 + 37 + 36 за скобки 36:

    39 + 37 + 36 = 36(33 + 3 + 1) = 36(27 + 3 + 1) = 36 • 31.

Мы представили сумму 39 + 37 + 36 в виде произведения двух целых чисел, одно из которых равно 31. Значит, данная сумма делится на 31.

Упражнения

654. Разложите на множители и сделайте проверку:

    а) mх + mу; б) kх - рх; в) -ab + ас; г) -mа - nа.

655. Вынесите за скобки общий множитель:

а) 5х + 5у;

б) 4а - 4b;

в) 3c+15d;

г) -6m - 9n;

д) ах + ау;

е) bc - bd;

ж) ab + а;

з) су - с;

и) -mа - а.

656. Представьте в виде произведения:

а) 7а+ 7у;

б) -8b + 8с;

в) 12х + 48y;

г) -9m - 27n;

д) 12а + 12;

е) -10 - 10с

657. Разложите на множители:

а) 7ах + 7bx;

б) 3by - 6b;

в) -5mn + 5n;

г) 3а + 9ab;

д) 5у2 - 15у;

е) 3х + 6х2;

ж) а2 - ab;

з) 8mn - 4m2;

и) -6ab + 9b2;

к) х2у - ху2;

л) ab - a2b;

м) -p2q2 - pq.

658. Вынесите за скобки общий множитель:

а) а2 + а;

б) x3 - х2;

в) с5 + с7;

г) а3 - а7;

д) 3m2 + 9m3;

е) 9р3 - 8р;

ж) 4с2 - 12с4;

з) 5х5 - 15х3;

и) -12у4 - 16y.

659. Представьте в виде произведения:

а) 14х + 21у;

б) 15а +10b;

в) 8ab - 6ас;

г)9ха + 9хb;

д)6аb - 3а;

е) 4х - 12х2;

ж)m4 - m2;

з) сx + с4;

и) 7х-14х3;

к) 16y3 + 12у2;

л) 18ab3- 9b4;

м) 4х3у2 - 6х2у3.

660. Найдите значение выражения:

    а) 3,28х - х2 при х = 2,28;

    б) а2у + а3 при а = -1,5 и у = -8,5;

    в) ау2 - у3 при а = 8,8 и у = -1,2;

    г) -mb - m2 при m = 3,48 и b = 96,52.

661. Решите уравнение:

а) х2 + 8х = 0;

б) 5х2 - х = 0;

в) 6y2 - 30у = 0;

г) 3х2 - 1,2х = 0;

д) 6х2 - 0,5х = 0

ж) х - 10х2 = 0;

з) 6х - 0,2х2 = 0;

<<< К началу      Окончание >>>

 

 

???????@Mail.ru