|
|
|
|
|
§ 10. Произведение одночлена и многочлена Вынесение общего множителя за скобки (окончание)662. Найдите корни уравнения:
1) Распределите, кто выполняет задания а), в), а кто — задания б), г), и выполните их. 2) Проверьте друг у друга правильность выполнения заданий. 3) Предложите друг другу составить задание, аналогичное заданию б). 664. Разложите на множители:
665. (Для работы в парах.) Докажите, что: а) 78 - 77 + 76 делится на 43; б) 213 - 210 - 29 делится на 13; в) 274 - 95 + 39 делится на 25; г) 164 - 213 - 45 делится на 110. 1) Распределите, кто выполняет задания а), в), а кто — задания б), г), и выполните их. 2) Проверьте друг у друга правильность выполнения заданий и исправьте ошибки, если они допущены. 3) Обсудите, какие свойства делимости использованы при выполнении задания. 666. Разложите на множители многочлен:
667. Представьте в виде произведения:
668. Вынесите за скобки общий множитель:
669. Разложите на множители многочлен:
670. Укажите общий множитель для всех слагаемых суммы и вынесите его за скобки:
672. Разложите на множители:
Упражнения для повторения 673. Велосипедист проехал путь АВ со скоростью 12 км/ч. Возвращаясь из B в A, он развил скорость 18 км/ч и затратил на обратный путь на 15 мин меньше, чем на путь из A в B. Сколько километров между А и B? 674. Решите уравнение:
675. Известно, что значение выражения а - b при некоторых значениях а и b равно 0,5. Чему равно при тех же а и b значение выражения: а) b - а; 676. Запишите в виде выражения: а) произведение разности а и b и их суммы; б) сумму квадратов а и b; в) квадрат суммы а и b; г) разность квадратов b и с; д) куб разности b и с; е) сумму кубов b и с.
|
|
|



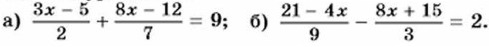
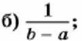 в) (а - b)2; г) (b - а)2; д) (а - b)3; е) (b - а)3?
в) (а - b)2; г) (b - а)2; д) (а - b)3; е) (b - а)3?