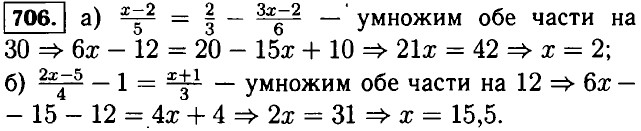|
|
|
|
Главная >> Решенния упражнений к учебнику Макарычева. Алгебра 7 класс |
|
|
Домашние работы Умножение многочлена на многочлен (окончание)692. а) (x - 3) (х + 7) - 13 = х2 + 7х - 3х - 21 - 13 = x2 + 4x - 34, (х + 8)(х- 4) - 2 = х2 - 4x + 8x - 32 - 2 = x2 + 4x - 34 ⇒ (x - 3)(x + 7) - 13 = (x + 8) (x - 4) - 2; б) 16 - (а + 3)(а + 2) = 16 - а2 - 2а - 3а - 6 = -а2 - 5а + 10, 4 - (6 + а)(а - 1) = 4 - 6а + 6 = -а2 + а = -а2 - 5а + 10 ⇒ 16 - (а + 3)(а + 2) = 4 - (6 + а)(а - 1). 693. а) (x - 5)(x + 8) - (x + 4)(x - 1) = x2 + 8x - 5x - 40 - x2 + x - 4x + 4 = -36 — не зависит от x; б) x4 - (x2 - 1)(x2 + 1) = x4 - x - x2 + x2 + 1 = 1 — не зависит от x. 694. (у - 6)(у + 8) - 2 • (у - 25) = у2 + 8у - 6у - 48 - 2у + 50 = у2 + 2, т. к. у2 ≥ 0, то у2 + 2 ≥ 2 принимает положительное значение при любом у. 695. а) n • (n - 1) - (n + 3)(n + 2) = n2 - n2 - 2n - 3n - 6 = -6n - 6 = - 6 • (n + 1) — делится на 6; б) n • (n + 2) - (n - 7)(n - 5) = n2 + 2n - n2 + 5n + 7n - 35 = 14n - 35 = 7 • (2n — 5) — делится на 7. 696. а - 2n + 1, b = 2n + 3, с = 2n + 5, d = 2n + 7 — четыре последовательных нечётных числа, cd - ab = (2n + 5)(2n + 7) - (2n + 1)(2n + 3) = 4n2 + 14n + 10n + 35 - 4n2 - 6n - 2n - 3 = 16n + 32 = 16 • (n + 2) - кратно 16. 697. а) (3x - 1)(5x + 4) - 15x2 = 17 ⇒ 15x2 + 12x - 5x - 4 - 15x2 = 17 ⇒ 7x = 21 ⇒ x = 3; б) (1 - 2x)(1 — 3x) = (6x - 1)x - 1 ⇒ 1 - 3x -2x + 6x2 = 6x2 - x - 1 ⇒ 1 - 5x = -x - 1 ⇒ 4x = 2 ⇒ x = 0,5; в) 12 - x • (x - 3) = (6 - x)(x + 2) ⇒ 12 - x2 + 3x = 6x + 12 - x2 - 2x ⇒ 6x - 2x - 3x = 12 - 12 ⇒ x = 0; г) (x + 4)(х + 1) = х - (х - 2) (2 - х) ⇒ х2 + х + 4х + 4 = х - 2х + х2 + 4 - 2х ⇒ х + 4х + 2х - х + 2х = 4 - 4 ⇒ х = 0; 698. а) 5 + х2 = (х + 1)(х + 6) ⇒ 5 + х2 = х2 + 6х + х + 6 ⇒ 7х = -1 ⇒ х = б) 2х • (х - 8) = (х + 1)(2х - 3) ⇒ 2х2 - 16х = 2х2 - 3х + 2х - 3 ⇒ 15x = 3 ⇒ х = 0,2; в) (3х - 2)(х + 4) - 3 • (х + 5)(х - 1) = 0 ⇒ 3х2 + 12x - 2x - 8 - 3х2 + 3х - 15х + 15 = 0 ⇒ 10х - 12х = 8 - 15 ⇒ -2х = -7 ⇒ х =3,5; г) х2 + х • (6 - 2х) = (х - 1)(2 - х) - 2 ⇒ х2 + 6х - 2х2 = 2х - x2 + х - 2 ⇒ 6х - 2х - х = -4 ⇒ 3х = -4 ⇒ х = 699. а) n • (n + 5) - (n - 3)(n + 2) = n2 + 5n - n2 - 2n + 3n + 6 = 6n + 6 = 6 • (n + 1); б) (n - 1 )(n + 1) - (n - 7)(n - 5) = n2 + n - n - 1 - n2 + 5n + 7n - 35 = 12n - 36 = 12 • (n - 3). 700. n, n + 1, n + 2 — три последовательных натуральных числа. Известно что, n2 + 65 = (n + 1)(n + 2) ⇒ n2 + 65 = n2 + 2n + n + 2 ⇒ 3n = 63 ⇒ n = 21, значит n = 21, n + 1 = 22, n + 2 - 23. Ответ: 21, 22, 23. 701. 2n + 1, 2n + 3, 2n + 5 — три последовательных нечётных числа. Известно что, (2n + 3)(2n + 5) - (2n +3)(2n + 1) = 76 ⇒ (2n + 3)(2n + 5 - 2n - 1) = 76 ⇒ 4 • (2n + 3) = 76 ⇒ 8n + 12 = 76 ⇒ n = 8, значит 2n + 1 = 17, 2n + 3 = 19, 2n + 5 = 21. Ответ: 17, 19, 21. 702. Пусть одна из сторон прямоугольника равна а, значит другая смежная её сторона равна 703. Пусть сторона квадрата равняется х. Известно что, х2 + 30 = (х + 3)(x - 2) ⇒ x2 + 30 = x + 3x - 2х - 6 ⇒ х = 36. Ответ: 36 см. 704. Пусть срок выполнения планового задания t дней. Известно что, 54t +18 = 60 • (t - 1) ⇒ 54t +18 = 60t - 60 ⇒ 6t = 78 ⇒ t = 13 ⇒ t - 1 = 12. Ответ: бригада работала 12 дней. 705. Пусть за t дней бригаде нужно было вспахать поле. Тогда поле было 112f га. Известно что, 112t = 120 • (t - 1) ⇒ St = 120 ⇒ t = 15 ⇒ 1121 = 1680. Ответ: 1680 га.
707. а) сумма квадратов а и b; б) квадрат суммы а и b; в) разность кубов а и 6; г) куб разности а и b.
|
|
|



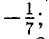
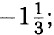
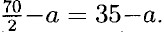 Известно что, а • (35 - а) + 50 = (а - 5)(35 - а + 5) ⇒ 35а - а2 + 50 = 40а - а2 - 200 + 5а ⇒ 10а = 250 ⇒ а = 25 ⇒ 35 - а = 10. Ответ: длина 25, ширина 10.
Известно что, а • (35 - а) + 50 = (а - 5)(35 - а + 5) ⇒ 35а - а2 + 50 = 40а - а2 - 200 + 5а ⇒ 10а = 250 ⇒ а = 25 ⇒ 35 - а = 10. Ответ: длина 25, ширина 10.