Умножение многочлена на многочлен

Умножим многочлен а + b на многочлен с + d. Составим произведение этих многочленов:

(а + b)(с + d).

Обозначим двучлен а + b буквой х и преобразуем полученное произведение по правилу умножения одночлена на многочлен:

(а + b)(c + d) = х(с + d) = хс + xd.

В выражение хс + xd подставим вместо х многочлен а + b и снова воспользуемся правилом умножения одночлена на многочлен:

хс + xd = (а + b)с + (а + b)d = ас + bс + ad + bd.

Итак,

(а + b)(с + d) = ас + bc + ad + bd.

Произведение многочленов а + b и с + d мы представили в виде многочлена ас + bc + ad + bd. Этот многочлен является суммой всех одночленов, получающихся при умножении каждого члена многочлена а + b на каждый член многочлена с + d.

Произведение любых двух многочленов можно представить в виде многочлена.

При умножении многочлена на многочлен пользуются правилом:

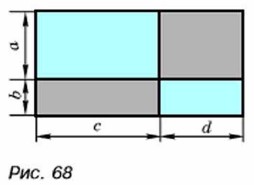
чтобы умножить многочлен на многочлен, нужно каждый член одного многочлена умножить на каждый член другого многочлена и полученные произведения сложить.

Заметим, что при умножении многочлена, содержащего m членов, на многочлен, содержащий n членов, в произведении (до приведения подобных членов) должно получиться mn членов. Этим можно пользоваться для контроля.

В древности справедливость некоторых равенств при положительных значениях переменных математики доказывали геометрически. Так, великий греческий математик Евклид в своём трактате «Начала» (III в. до и. э.) справедливость равенства (а + b)(c + d) = ас + bc + ad + bd доказывал с помощью чертежа, изображённого на рисунке 68.

Пример 1. Умножим многочлен 4х²2² + 2ху - у² на многочлен 2х - у.

Имеем

(4х² + 2ху - у²)(2х - у) = 8х² + 4х²у - 2xy² - 4х²у - 2ху² + у³ = 8х³ - 4ху² + у³.

Пример 2. Упростим выражение (2а - 3)(5 - а) - 3а(4 - а).

Имеем

(2а - 3)(5 - а) - 3а(4 - а) = 10а - 15 - 2а² + 3а - (12а - 3а²) = 13а - 15 - 2а² - 12а + 3а² = а² + а - 15.

Пример 3. Докажем, что при любом натуральном п значение выражения n(n - 5) - (n - 14) (n + 2) кратно 7.

Выполним преобразование:

n(n -5) - (n - 14)(n + 2) = n² - 5n - (n² - 14n + 2n - 28) = n² - 5n - n² + 14n - 2n + 28 = 7n + 28 = 7(n + 4).

При любом натуральном л произведение 7(n + 4) делится на 7, а значит, и значение выражения n(n - 5)-(n - 14)(n + 2) делится на 7.

Продолжение >>>