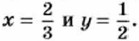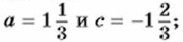Разложение многочлена на множители способом группировки (окончание)

712. Представьте в виде произведения многочлен:

а) mn - mk + xk - хn;
б) х² + 7х - ах - 7а;

в) 3m - mk + 3k - k²;
г) xk - ху - х² + yk.

713. Найдите значение выражения:

а) p²q² + pq - q³ - р³ при р = 0,5 и q = -0,5;

б) 3х³ - 2y³ - 6х²у² + ху при

714. Чему равно значение выражения:

а) 2 а + ас² - а²с - 2с при

б) х²у - у + ху² - х при х = 4 и у = 0,25?

715. Докажите тождество:

а) ах - у + х - ay = (х - у)(а + 1);

б) ах - 2bу + ау - 2bх = (а - 2b)(х + у).

716. Представьте в виде произведения:

а) ас² - ad + с³ - cd - bc² + bd;

б) ах² + ay² - bx² - by² + b - a;

в) an² + cn² - ap + ap² - cp + cp²;

г) xy² - by² - ax + ab + y² - a.

717. Разложите на множители многочлен:

а) х²у + х + ху² + у + 2ху + 2; б) х² - ху + х - ху² + у³ - у².

718. Разложите на множители трёхчлен:

а) х² + 6х + 5; б) х² - х - 6; в) а² - 5а + 4; г) а² - 6а - 16.

Упражнения для повторения

719. Число коров в стаде возросло на 60 голов, а в связи с улучшением кормовой базы удой молока от одной коровы возрос в среднем с 12,8 л в день до 15 л. Сколько коров стало в стаде, если ежедневно стали получать на 1340 л молока больше, чем раньше?

720. Решите уравнение:

а) 4 - х(х + 8) = 11 - х²; б) 4х(3х - 1) - 2х(6х + 8) = 5.

721. Запишите в виде выражения:

а) квадрат разности х и у;

б) сумму числа 3 и произведения а и b;

в) разность числа 7 и удвоенного произведения а и b.

Контрольные вопросы и задания

1. Сформулируйте правило умножения многочлена на многочлен.

2. Представьте в виде многочлена произведение многочленов х - 2у и ху + 4.

3. На примере многочлена ab - 2b + 5а - 10 объясните, как выполняется разложение многочлена на множители способом группировки.

<<< К началу Решенния >>>