|
|
|
|
Главная >> Домашние работы к учебнику Макарычева. Алгебра 7 класс |
|
|
Решенния упражнений Дополнительные упражнения к параграфу 11787. Пусть сторона получившегося квадрата равна х. Тогда длина исходного прямоугольника х + 4, а ширина х - 5. Значит х2 - 40 = (х + 4)(х - 5) ⇒ х2 - 40 = х2 - 5х + 4х - 20 ⇒ х = 20 ⇒ (х + 4)(х - 5) = 24 • 15 = 360 см2. Ответ: 360 см2. 788. Пусть длина прямоугольника равняется а, ширина — b, а + b — половина периметра а + b = 789. Пусть ширина прямоугольника равна а, тогда длина 790. а) а + ab - 7а - 7b = а • (а + b) - 7 • (а + b) = (а - 7)(а + b): при а = 6,6 и b = 0,4 ⇒ (а - 7)(а + b) = (6,6 - 7) • (6,6 + 0,4) = -0,4 • 7 = -2,8; б) х2 - ху - 4х + 4у = х • (х - у) - 4 • (х - у) = (х - 4)(x • у): при х = 0,5 и у - 2,5 ⇒ (х - 4)(х - у) - (0,5 - 4)(0,5 - 2,5) = 3,5 • 2 = 7; в) 5а2 - 5ах - 7а + 7х = 5а • (а - х) - 7 • (а - х) = (5а - 7)(а - х): при а - 4 и х = -3 ⇒ (5а - 7)(а - х) = (5 • 4 - 7) (4 + 3) = 13 • 7 = 91; г) xb - xc + 3c - 3b = х • (b - с) - 3 • (b - с) = (х - 3)(b - с): при х = 2, b - 12,5 и с = 8,3 ⇒ (x - 3)(b — с) = (2 - 3) (12,5 - 8,3) = -4,2; д) ау - ах - 2х + 2у = а • (у - x) + 2 • (у - x) = (а + 2)(у - х): при а = -2, х - 9,1 и у = -6,4 ⇒ (а - 2)(у - х) = (-2 + 2)(-6,4 - 9,1) = 0; е) 3ах - 4by - 4ay + 3bx = 3x • (а + b) - 4y • (а + b) = (3x - 4у)(а + b): при а = 3, b = -13, x = -1 и у - 2 ⇒ (3x - 4у)(а + x) = (-3 + 8)(3 - 13) = -5 • 10 = -50. 791. а) а3 - 2а2 + 2а - 4 = а2 • (а - 2) + 2 • (а - 2) = (а2 + 2) (а - 2); б) х3 - 12 +6b2 - 2x = х2 • (х + 6) - 2 • (x + 6) = (х2 - 2)(а; + 6); в) с4 - 2с2 + с3 - 2с = c3 • (c + 1) - 2с • (с + 1) = (с3 - 2с)(с + 1); г) -у6 - у5 + у4 + у3 = -y5 • (у + 1) + у3 • (у +1) = (у3 - у5)(у + 1); д) а2b - b2с + а2с - bс2 = а2 • (b + с) - bс • (b + с) = (а2 - bс)(b + с); е) 2x3 + ху2 - 2x2у - у3 = 2x2 • (x - у) + у2 • (х - у) = (2х2 + у2)(х - у); ж) 16аb2 - 10с3 + 32ас2 - 5b2с = 16а • (b2 + 2с2) - 5с • (b2 + 2с2) = (16а - 5с) (b2 + 2с2); з) 6а3 - 21а2b + 2аb2 - 7b3 = 2а • (3а2 + b2) - 7b • (3а2 + b2) - (2а - 7b)(3а2 + b2). 792. а) mа - mb + nа — nb + pa - pb = m • (а - b) + n • (а - b) + р • (а - b) = (m + n + р)(а - b); 6) ах - bx - сх + ay — by - су = х • (а - b - с) + у • (а - b - с) = (x + у)(а - b - с); в) х2 + ах2 - у - ау + сх2 - су = х2 • (1 + а + с) - у • (1 + а+с) = (х2 - у)(1 + а + с); г) ах2 + 2у - bх2 + ay + 2х2 - by - х2 • (а — b + 2) + у • (2 + а - b) = (х2 + у)(а - b + 2). 793. а) х2 - 10x + 24 = х2 - 6х - 4х + 24 - х • (х - 4) - 6 • (х - 4) - (х - b)(х - 4); б) х2 - 13x + 40 = х2 - 5х - 8х + 40 = х • (х - 5) - 8 • (х - 5) = (х - 8)(х - 5); в) х2 + 8x + 7 = х2 + 7х + х + 7 = х • (х + 7) + (х + 7) - (х + 1)(x + 7); г) х2 + 15х + 54 = х2 + 9х + 6х + 54 = х • (х + 9) + б • (х + 9) = (х + b)(х + 9); д) х2 + х - 12 - х2 - 3х + 4х - 12 = х • (х - 3) + 4 • (х - 3) = (х + 4)(х - 3); е) х2 - 2х - 35 = х2 - 7х + 5х - 35 = х • (х - 7) + 5 • (х - 7) = (х + 5)(х - 7). 794. а) а • (х + b) + х • (х - 3а) при х = 2а - 3 ⇒ а • (2а - 3 + 6) + (2а - 3)(2а - 3 - 3а) = а • (2а + 3) + (2а - 3) (-а - 3) = 2а2 + 3а - 2а2 - 6а + 3а + 9 = 9; б) х • (х - 3а) + а • (а + х) + 4 при х = а + 3 ⇒ (а + 3)(а + 3 - 3а) + а • (а + а + 3) + 4 = (а + 3) (3 - 2а) + а • (2а + 3) + 4 - 3а - 2а2 + 9 - 6а + 2а2 + 3а + 4 = 9 + 4 = 13. 795. а) (у4 + у3)(у2 - у) = у3 • (у + 1) • у • (у - 1) = у4 • (у + 1)(у - 1); б) (а2 + 3а)(а3 + 3а + 2) = а • (а + 3) (а2 + а + 2а + 2) = а • (а + 3)(а,(а + 1) + 2,(а+1)) = а • (а + 3)(а + 2)(а + 1) = а • (а + 1)(а + 2)(а + 3); в) (а2 + аb + b2)(а2 - аb + b2) = а4 - а3b + а2b2 + а3b - а2b2 + аb3 + а2b2 - аb3 + b4 = а4 + а2b2 + b2; г) (с4 - с2 + 1)(с4 + с2 + 1) = с8 + с6 + с4 - с6 - с4 - с2 + с4 + с2 + 1 = с8 + с4 + 1. 796. (х3 + 4х2 - 17х + 41)(х + а) = х4 + 4х3 - 17х2 + 41х + ах3 + 4ах2 - 17ах + 41а. Чтобы многочлен не содержал х3 необходимо, чтобы выполнялось равенство: 4х3 + ах3 = 0. Значит а = -4. 797. Если b + с = 10, то (10а + b) (10а + с) = 100а2 + 10са + 10аb + bс = 100а2 + 10а • (с + b) + bс = 100а2 + 100а + bс = 100а • (а + 1) + bс: а) 23 • 27 = 100 • 2 • (2 + 1) + 3 • 7 = 200 • 3 + 21 = 621; б) 42 • 48 = 100 • 4 • (4 + 1) + 2 • 8 = 400 • 5 + 16 = 2016; в) 59 • 51 = 100 • 5 • (5 + 1) + 9 • 1 = 500 • 6 + 9 = 3009; г) 84 • 86 = 100 • 8 • (8 + 1) + 6 • 4 = 800 • 9 + 24 = 7224. 798. а) (а + с)(b + с) + (а - c)(b - с) = ab + ас + cb + с2 + ab - ас - cb + с2 = 2ab + 2с2 = 2 • (ab + с2): при ab + с2 = 0 ⇒ 2 • (аb + с2) = 0; б) (a + 1)(b + 1) - (а - 1)(b - 1) = ab + a + b + 1-ab + a + b - 1 = 2а + 2b = 2 • (а + b): при а + b = 9 ⇒ 2 • (а + b) = 18.
|
|
|



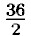 = 18. Значит (а+1)(5 + 2) = аb + 30 ⇒ аb + 2а + b + 2 = аb + 30 ⇒ 2а, + b = 28 ⇒ а + b = 18 ⇒ b = 18 - а ⇒ 2а + 18 - а = 28 ⇒ а = 10 ⇒ b = 18 - а = 8 ⇒ ab = 80 м2. Ответ: 80 м2.
= 18. Значит (а+1)(5 + 2) = аb + 30 ⇒ аb + 2а + b + 2 = аb + 30 ⇒ 2а, + b = 28 ⇒ а + b = 18 ⇒ b = 18 - а ⇒ 2а + 18 - а = 28 ⇒ а = 10 ⇒ b = 18 - а = 8 ⇒ ab = 80 м2. Ответ: 80 м2.
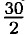 - а = 15 - а. Значит (а + 5) (15 - а - 3) + 8 = а • (15 - а) ⇒ 12а - а2 + 60 - 5а + 8 = 15а - а2 ⇒ 8а = 68 ⇒ а = 8,5 ⇒ 15 - а = 6,5 ⇒ а • b = 55,25 см2. Ответ: 55,25 см2.
- а = 15 - а. Значит (а + 5) (15 - а - 3) + 8 = а • (15 - а) ⇒ 12а - а2 + 60 - 5а + 8 = 15а - а2 ⇒ 8а = 68 ⇒ а = 8,5 ⇒ 15 - а = 6,5 ⇒ а • b = 55,25 см2. Ответ: 55,25 см2.