Возведение в квадрат и в куб суммы и разности двух выражений

При умножении многочлена на многочлен каждый член одного многочлена умножают на каждый член другого. Однако в некоторых случаях умножение многочленов можно выполнить короче, воспользовавшись формулами сокращённого умножения.

Возведём в квадрат сумму а + b. Для отого представим выражение (а + b)² в виде произведения (а + b)(а + b) и выполним умножение:

(а + b)² = (а + b)(а + b) = a² + ab + ab + b² = а² + 2ab + b².

Значит,

(а + b)² = а² + 2 аb + b². (1)

Тождество (1) называют формулой квадрата суммы. Эта формула позволяет проще выполнять возведение в квадрат суммы любых двух выражений:

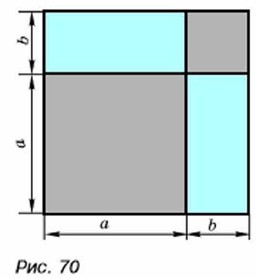
квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого и второго выражений плюс квадрат второго выражения.

В «Началах» Евклида справедливость равенства

(а + b)² = а² + 2ab + b²

при положительных значениях а и b доказана геометрически с помощью чертежа, приведённого на рисунке 70.

Возведём в квадрат разность а - b, получим

(а - b)² = (а - b)(a - b) = а² - ab - ab + b² = а² - 2ab + b².

Значит,

(а - b)² = а² - 2 аb + b². (2)

Тождество (2) называют формулой квадрата разности. Она позволяет проще возводить в квадрат разность любых двух выражений:

квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого и второго выражений плюс квадрат второго выражения.

Заметим, что тождество (2) можно получить из тождества (1), если представить разность а - b в виде суммы а + (-b):

(а - b)² = (а + (-b))² = а² + 2а (-b) + (-b)² = а² - 2аb + b².

Приведём примеры применения формул квадрата суммы и квадрата разности.

Пример 1. Возведём в квадрат сумму 8х + 3.

Но формуле квадрата суммы получим

(8х + 3)² = (8х)² + 2 • 8х • 3 + 3² = 64х² + 48x + 9.

Пример 2. Возведём в квадрат разность 10х - у.

Воспользовавшись тождеством (2), получим

(10x - у)² = (10х)² - 2 • 10x • y + y² = 100х² - 20ху + у².

Пример 3. Представим в виде многочлена выражение (-5а - 4)².

Выражение (-5а - 4)² тождественно равно выражению (5а + 4)². Действительно, при любом а значениями выражений -5а - 4 и 5а + 4 являются противоположные числа, а квадраты противоположных чисел равны. Получаем

(-5а - 4)² = (5а + 4)² = 25а² + 40а +16.

Пример 4. Упростим выражение 2х(3 + 8х) - (4х - 0,5)².

2х(3 + 8х) - (4х - 0,5)² = 6х + 16х² - (16х² - 4х + 0,25) = 6x + 16х² - 16х² + 4х - 0,25 = 10х - 0,25.

Зная формулы квадрата суммы и квадрата разности, нетрудно вывести формулы куба суммы и куба разности. Имеем

(а + b)³ = (а + b)²(a + b) = (а² + 2ab + b²)(а + b) = а³ + 2a²b + ab² + а²b + 2ab² + b³ = а³ + 3а²b + 3аb² + b³.

Следовательно,

(а + b)³ = а³ + 3а²b + 3аb² + b³. (3)

Тождество (3) называют формулой куба суммы.

Куб суммы двух выражений равен кубу первого выражения плюс утроенное произведение квадрата первого выражения и второго плюс утроенное произведение первого выражения и квадрата второго плюс куб второго выражения.

Аналогично можно получить, что

(а - b)³ = а³ - 3а²b + 3аb² - b³. (4)

Тождество (4) называют формулой куба разности.

Куб разности двух выражений равен кубу первого выражения минус утроенное произведение квадрата первого выражения и второго плюс утроенное произведение первого выражения и квадрата второго минус куб второго выражения.

Заметим, что тождество (4) можно получить из тождества (3), если разность а - b представить в виде суммы а + (-b).

Продолжение >>>