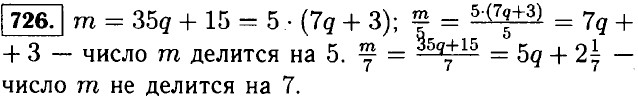Деление с остатком

722. а) 138 = 19 • 7 + 5 — частное 19, остаток 5; б) -16 = -6 • 3 + 2 — частное -6, остаток 2; в) -4 = -1 • 5 + 1 — частное —1, остаток 1.

723. -10 = -1 • 11 + 1.

724. -11, -4, 3, 10; -11 = -2 • 7 + 3; -4 = -1 • 7 + 3; 3 = 0 • 7 + 3; 10 = 1 • 7 + 3.

725. В году 365 дней, пусть год начинается с воскресенья, значит нужно подсчитать, сколько недель в 364 днях: 364 : 7 = 52. А в 52 неделях 52 воскресенья. Значит максимальное количество воскресений в году 53.

727. Пусть искомое число а = bc + d. Предположим что все числа a, b, с, d — не чётные, значит произведение bс — тоже не чётное, тогда сумма bc + d — чётное, значит а должно быть чётным, противоречие, а, b, с, d не могут быть все не чётными.

728. Пусть искомые числа: а = 3q + 1; b = 3s + 2. Так как ab + 1 = (3q + 1)(3s + 2) + 1 = 9qs + 3s + 3q + 2 + 1 = 3 • (3qs + s + q +1) — кратно 3.

729. Да, верно, ab • (a + b)(a - b) — если а или b делится на 3, то очевидно, что произведение кратно 3. Если а и b не делятся на 3, тогда остаток от деления равен 1 или 2. Если остатки одинаковы, тогда а - b кратно 3, если же один равен 1, а другой 2, тогда а + b, делится на делится на 3.

730. а = 12q + 5 = 4 • 3 • + 4 • 1 + 1 = 4 • (3q +1) + 1 — остаток равен 1.

731. Пусть первое число а = 9q + 7, а второе х = 9у + 5; ах = (9q + 7)(9у + 5) = 81 qy + 45q + 63у + 9 • 3 + 8 = 9 • (9qy + 5q + 7у + 3) + 8 — остаток 8.

732. Пусть искомое число а, тогда а = 5 • (q + 4) + 1; и а = 7q + 1. Значит 5 • (q + 4) + 1 = 7q + 1 ⇒ bq + 21 = 7q + 1 ⇒ 2q = 20 ⇒ q = 10 ⇒ a = 7q + 1 = 71. Ответ: 71.

733. Докажем сначала делимость 2 произведения n • (2n + 1)(7n + 1). При n нечётном сумма 7n + 1 является чётным числом. При n чётном очевидно, что произведение кратно 2. Осталось доказать делимость на 3. Рассмотрим 3 случая:

1) n делится на 3, очевидно, что и произведение делится на 3.

2) n даёт остаток при делении на 3 равный 1. Значит число n можно представить в виде n = 3q + 1. Докажем что при таком значении n сумма 2n +1 кратна 3. Так как 2 • (3q + 1) + 1 = 6q + 2 + 1 = 6q + 3 = 3 • (2q + 1), значит и n • (2n + 1)(7n + 1) — кратно 3.

3) n даёт остаток при делении на 3 равный 2. Значит число n можно представить в виде n = 3q + 2. Докажем что при таком значении п сумма 7n + 1 кратна 3. Так как 7 • (3q + 2) + 1 = 21q + 14 + 1 = 21q + 15 = 3 • (7q + 5), значит и n • (2n + 1)(7n + 1) — кратно 3.

<<< К началу