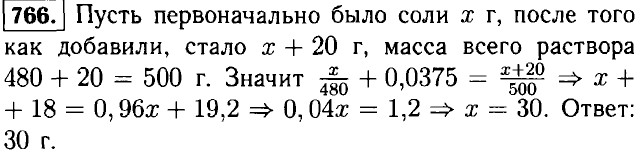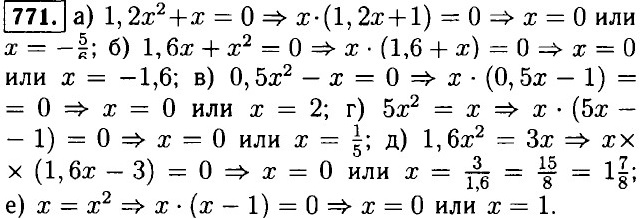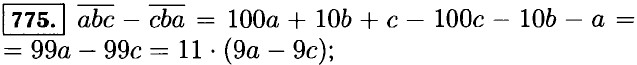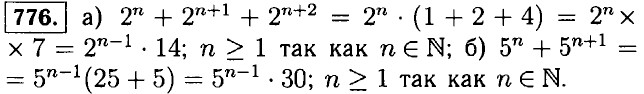Дополнительные упражнения к параграфу 10 (окончание)

763. Пусть кооператив должен был изготавливать по х сорочек каждый день, тогда он выпускал х + 10 сорочек в день. Значит 7 • (х + 10) = 8х ⇒ х = 70. Ответ: 70 сорочек.

764. Пусть х т пшеницы было первого сорта, тогда 1400—х второго сорта. Значит 0,98х + 0,97 • (1400 - х) = 1364 ⇒ 0,98х + 1358 - 0,97х = 1364 ⇒ 0,01х = 6 ⇒ х = 600 ⇒ 1400 - х = 800. Ответ: 600 т и 800 т.

765. Пусть бригада должна была закончить работу через t дней. Значит 80t = (80 + 10)(t -1) + 30 ⇒ 80t = 90t - 90 + 30 ⇒ 10t = 60 ⇒ t = 6 ⇒ 80t = 480. Ответ: 480 га.

767. а) а₂₀ - а₁₀ + а₅ - а₅ • (а₁₅ - а₅ + 1) = а5 • (1 + а₅ • (а₁₀ - 1)); б) b₆₀ + b₄₀ - b₂₀ = b₂₀(b₄₀ + b₂₀ - 1) = b₂₀b₂₀b₂₀ + 1) - 1); в) а₁₀ - а₈ - а₆ = а₆ • (а₄ - а₂ - 1) = а₆ • (а₂ • (а₂ - 1) - 1); г) b₄₀ + b₂₀ + b₁₀ = b₁₀(b₃₀ + b₁₀ + 1) = b₁₀(b₁₀(b₂₀ + 1) + 1).

768. a) 7₁₆ + 7₁₄ = 7₁₄(7₂ + 1) = 7₁₄ • 50; б) 5₃₁ - 5₂₉ = 5₂₉(5₂ - 1) = 5₂₉ • 24 - 5₂₇ • 600; в) 25₉ + 5₁₇ = 5₁₈ + 5₁₇ = 5₁₆(25 + 5) = 5₁₆ • 30; г) 27₁₀ - 9₁₄ = 3₃₀ - 3₂₈ = 3₂₈(3₂ - 1) = 3₂₈ • 8 = 3₂₇ • 24; д) 12₁₃ - 12₁₂ + 12₁₁ = 12₁₁(12₂ - 12 + 1) = 12₁₁ (144 - 11) = 12₁₁ • 19 • 7; е) 11₉ - 11₈ + 11₇ = 11₇ • (11₂ - 11 + 1) = 11₇ • (121 - 10) = 11₇ • 37 • 3.

769. а) (а - 3b)(а + 2b) + 5а • (а + 2b) = (а + 2b)(а - 3b + 5а) = 3 • (а + 2b)(2а - b); б) (х + 8у)(2х - 5b) - 8у • (2х - 5b) = (х + 8у - 8у)(2х - 5b) = х • (2х - 5b); в) 7а₂ • (а - х) + (6а₂ - ах) (х - а) = 7а₂ • (а - х) + (ах - 6а₂)(а - х) = (а - х) (7а₂ + ах - 6а₂) = (а - х)(а₂ + ах); г) 11b₂ • (3b - у) - (6у - 3b₂)(у - 3b) = 11b₂ • (3b - у) - (3b₂ - 6у)(3b - у) = (11b₂ - 3b₂ + 6у)(3b - у) = 2 • (4b₂ + 3у)(3b - у).

770. а) 5сх + с₂ = с • (5x + с): при х = 0,17 и с = 1,15 ⇒ с • (5x + c) = 1,15 • (5 • 0,17 + 1,15) = 1,15 • (0,85 + 1,15) = 1,15 • 2 = 2,3;

б) 4а₂ - аb = а • (4а - b): при а = 1,47 и b = 5,78 ⇒ а • (4а - b) = 1,47 • (4 • 1,47 - 5,78) = 1,47 • (5,88 - 5,78) = 1,47 • 0,1 = 0,147.

772. а) (3а + b)₂ = (3 • (а + 2))₂ = 3₂ • (а + 2)₂ = 9 • (а + 2)₂; б) (12b - 4)₂ = (4 • (3b - 1))₂ = 4₂ • (3b - 1)₂ = 16 • (3b - 1)₂; в) (7х + 7у)₂ = 7₂ • (х + у)₂ = 49 • (х + у)₂; г) (-3р + b)₃ = 3₃ • (-р + 2)₃ = 27 • (-р + 2)₃; д) (5q - 30)₃ = 5₃ • (q - b)₃ = 125 • (q - b)₃; е) (2а - 8)₄ = 2₄ • (а - 4)₄ = 16 • (а - 4)₄.

773. Имеем а₂ - а = а • (а - 1). При чётном а очевидно, что произведение делится на 2. При не чётном а, а - 1 — чётное число, значит произведение а • (а - 1) при любом целом а делится на 2.

774. Имеем а₂ + а = а • (а + 1). При чётном а очевидно, что произведение делится на 2. При не чётном а, а + 1 — чётное число, значит произведение а • (а + 1) при любом целом а делится на 2.

<<< К началу