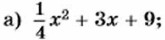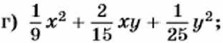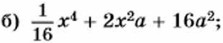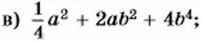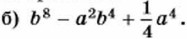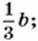Главная >> Алгебра 7 класс. Макарычев. ГДЗ

§ 12. Квадрат суммы и квадрат разности

Разложение на множители с помощью формул квадрата суммы и квадрата разности (окончание)

842. Сравните с нулем значение выражения:

    а) х2 - 30х + 225; б) -х2 + 2ху - у2.

843. Поставьте вместо многоточия какой-либо из знаков ≥ или ≤ так, чтобы получившееся неравенство было верно при любом значении х:

а) х2 - 16х + 64 ... 0;

б) 16 + 8х + х2 ... 0;

в) -х2 - 4х - 4 ... 0;

г) -х2 + 18х - 81 ... 0.

844. Представьте выражение в виде квадрата двучлена, если это возможно:

б) 25а2 - 30ab + 9b2;

в) р2 - 2р + 4;

д) 100b2 + 9с2 - 60bc;

е) 49х2 + 12xiy + 64у2.

845. Преобразуйте выражение в квадрат двучлена:

а) х4 - 8х2y2 + 16y4;

г) а2х2 - 2аbх + b2.

846. Разложите на множители трёхчлен:

    а) 4а6 - 4а3b2 + b4;

847. Докажите, что при любом значении х многочлен х2 + 6х + 10 принимает положительные значения.

848. Докажите, что выражение принимает лишь положительные значения:

а) х2 + 2х + 2;

б) 4у2 -4у + 6;

в) а2 + b2 - 2ab + 1;

г) 9х2 + 4 - 6ху + 4у2.

Упражнения для повторения

849. Прочитайте выражение:

    а) (а - 10b)2; б) а2 - (10b)2; в) (а + 10b) (а - 10b).

850. Запишите в виде выражения:

    а) квадрат суммы 3а и

    б) сумму квадратов 0,5m и 5,3n;

    в) произведение 0,6х2 и 9у2.

851. Представьте в виде многочлена:

    а) (х2 + 4ху - у2)(2у - х);

    б) (3 - а)(а3 - 4а2 - 5а);

    в) (а2 - 4аb + b2)(2а - b);

    г) (х - р)(х2 + рх + р2).

852. Представьте выражение в виде квадрата одночлена:

а) 4х4;

б) 0,25а4;

в) 36m6;

г) а2b4;

д) 9а4b2;

е) 0,16x6y4.

853. Преобразуйте в многочлен выражение: а) (3 + а)3; б) (х - 2)3.

Контрольные вопросы и задания

1. Напишите формулу квадрата суммы. Проведите доказательство.

2. Напишите формулу квадрата разности. Проведите доказательство.

3. Приведите пример трёхчлена, который можно представить в виде квадрата суммы.

4. Приведите пример трёхчлена, который можно представить в виде квадрата разности.

5. Напишите формулу куба суммы. Возведите в куб двучлен а + 2b.

6. Напишите форму куба разности. Возведите в куб двучлен 3х - у.

<<< К началу      Решенния >>>

 

 

???????@Mail.ru