|
|
|
|
Главная >> Домашние работы к учебнику Макарычева. Алгебра 7 класс |
|
|
Решенния упражнений
Разложение на множители с помощью формул квадрата суммы и квадрата разности833. а) х2 + 2ху + у2 = (х + у)2; б) р2 - 2pq + q2 = (р - q)2; в) а2 + 12а + 36 = (а + b)2; г) 64 + 16b + b2 = (8 + 6)2; д) 1 - 2z + z2 = (1 — z)2; е) n2 + 4n + 4= (n + 2)2.
835. а) 81а2 - 18аb + b2 = (9а - b)2; б) 1 + у2 - 2у = (1 - у)2; в) 8аb + b2 + 16а2 = (b + 4а)2; г) 100x2 + у2 + 20ху = (10x + у)2; д) b2 + 4а2 - 4аb - (b - 2а)2; е) 28ху + 49х2 + 4у2 = (7х + 2у)2.
837. а) (3b + 2а)2 = 9b2 + 12аb + 4а2; б) (3x + 7у)2 = 9x2 + 42xу + 49у2. 838. а) b2 + 20b + 100 = (b + 10)2; б) b2 + 14b + 49 = (b + 7) ; в) 16x2 + 24xу + 9у2 = (4x + 3у) ; г) 9р2 - 42ру + 49у2 = (3р - 7у)2. 839. а) -1 + 4а - 4а 2= -(1 - 4а + 4а2) = -(1 - 2а)2; б) -42а + 9а2 + 49 = (3а - 7)2; в) 24аb - 16а2 - 9b2 = -(16а2 - 24аb + 9b2) = -(4а - 3b)2; г) -44аx + 121а2 + 4x2 = (11а - 2x)2; д) 4cd - 25с2 - 0,16d2 = -(25с2 - 4cd + 0,16d2) = -(5с - 0,4d)2; е) -0,49x2 - 1,4xу - у2 = -(0,49x2 + 1,4xу + у2) = -(0,7л + у)2. 840. а) у2 - 2у + 1 = (у - 1)2: при у = 101 ⇒ (у - 1)2 = (101 - 1)2 = 1002 = 10000; при у = -11 ⇒ (у - 1)2 = (-11 - 1)2 = (-12)2 = 144; при у = 0,6 ⇒ (у - 1)2 = (0,6 - 1)2 = (-0,4)2 = 0,16; б) 4x2 - 20x + 25 = (2x - 5)2: при x = 12,5 ⇒ (2x - 5)2 = (2 • 12,5 - 5)2 = 202 = 400; при x = 0 ⇒ (2x - 5)2 = (2 • 0 - 5)2 = (-5)2 = 25; при х = -2 ⇒ (2x - 5)2 = (2 • (-2) - 5)2 = (-4 - 5)2 = (-9)2 = 81; в) 25а2 + 49 + 70а = (5а + 7)2: при а = 0,4 ⇒ (5а + 7)2 = (5 • 0,4 + 7)2 = (2 + 7)2 = 92 = 81; при а = -2 ⇒ (5а + 7)2 = (-2 • 5 + 7)2 = (-10 + 7)2 = • (-3)2 = 9; при а = -1,6 ⇒ (5а + 7)2 = (-1,6 • 5 +7)2 = (-8 + 7)2 = 1. 841. а) верно; б) x2 + 20x + 100 = (x + 10)2 ≥ 0: при x = -10; (x + 10)2 = 0 — не верно. 842. а) x2 - 30x + 225 - (x - 15)2 ≥ 0; б) -x2 + 2xу - у2 = -(x2 - 2xу + у2) = -(x - у)2 ≤ 0. 843. a) x2 - 16x + 64 = (x - 8)2 ≥ 0; 6) 16 +8x + x2 = (4 + x)2 ≥ 0; в) -x2 - 4x - 4 = -(x2 + 4x + 4) = -(x + 2)2 ≤ 0; г) -x2 + 18x - 81 = -(x2 - 18x + 81) = -(x - 9)2 ≤ 0.
847. х2 + 6х +10 = х2 + 6х + 9 +1 = (х + 3)2 +1 ≥ 1 848. а) х2 + 2х + 2 = х2 + 2х + 1 + 1 = (х + 1)2 + 1 ≥ 1; б) 4у2 - 4у + 6 = 4у2 - 4у + 1 + 5 = (2у - 1)2 + 5 ≥ 5; в) а2 + b2 - 2аb + 1 = (а - b)2 + 1 ≥ 1; г) 9х2 + 4 - 6ху + 4у2 = (9х2 - 6ху + у2) + 3у2 + 4 = (3х - у)2 + 3у2 + 4 ≥ 4. 849. а) квадрат разности а и 106; б) разность квадратов а и 10b; в) произведение суммы а и 10b и разности а и 10b. 850. 851. а) (х2 + 4ху - у2)(2у - х) = 2х2у - х3 + 8ху2 - 4х2у - 2у3 + ху2 = -х3 - 2х2у + 9ху2 - 2у3; б) (3 - а)(а3 - 4а2 - 5а) = 3а3 - 12а2 - 15а - а4 + 4а3 + 5а2 = 7а3 - 7а2 - 15а - а4; в) (а2 - 4аb + b2)(2а - b) = 2а3 - а2b - 8а2b + 4аb2 + 2аb2 - b3 = 2а3 - 9а2b + 6аb2 - b3; г) (х — р ) (х2 + рх + р2) = х3 + рх2 + р2х - рх2 - р2х - р3 = x3 - p3. 852. а) 4х4 = (2х2)2; б) 0,25а4 = (0,5а2)2; в) 36m6 = (6m3)2; г) а2b4 = (аb2)2; д) 9а4b2 = (3а2b)2; е) 0,16х6у4 - (0,4х3у2)2. 853. а) (3 + а)3 = 27 + 27а + 9а2 + а3; б) (х - 2)3 = х3 - 6х2 + 12х - 8.
|
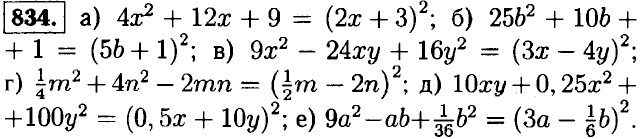
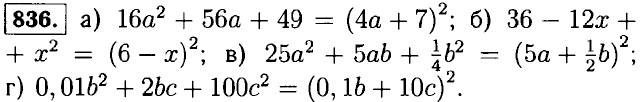
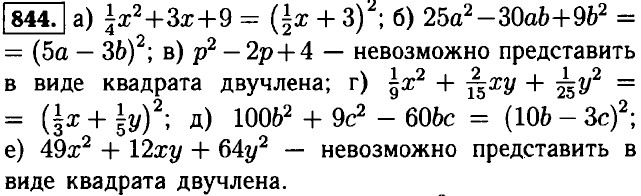
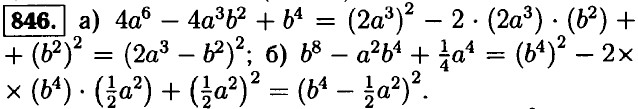
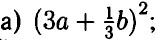б) (0,5m)2 + (5,3n)2; в) (0,6х2) • (9у2).
|
|