Умножение разности двух выражений на их сумму

Рассмотрим ещё одну формулу сокращённого умножения. Умножим разность а - b на сумму а + b:

(а - b)(a + b) = а² + ab - ab - b² = а² - b².

Значит,

(а - b)(а + b) = а² - b². (1)

Тождество (1) позволяет сокращённо выполнять умножение разности любых двух выражений на их сумму:

произведение разности двух выражений и их суммы равно разности квадратов этих выражений.

Приведём примеры применения формулы (1).

Пример 1. Умножим разность 3х - 7у на сумму 3х + 7у.

Воспользовавшись тождеством (1), получим

(3х - 7у)(3х + 7у) = (3х)² - (7у)² = 9х² - 49у².

Пример 2. Представим в виде многочлена произведение

(5а² - b³) (5а² + b³).

Применив тождество (1), получим

(5а² - b³)(5а² + b³) = (5а²)² - (b³)² = 25а⁴ - b⁶.

Пример 3. Представим в виде многочлена произведение

(-2а - 9с) (2а - 9с).

Вынесем в выражении -2а - 9с за скобки -1, тогда

(-2а - 9с)(2а - 9с) = (-1)(2а + 9с) (2а - 9с) = -((2а)² - (9с)²) = -(4а² - 81с²) = -4а² + 81с².

Преобразование можно выполнить иначе:

(-9с - 2а)(-9с + 2а) = (-9с)² - (2а)² = 81с² - 4а².

Пример 4. Упростим выражение 6,5х² - (2х + 0,8)(2х - 0,8).

Имеем

6,5x² - (2х + 0,8)(2х - 0,8) = 6,5х² - (4х² - 0,64) = 6,5х² - 4х² + 0,64 = 2,5х² + 0,64.

Упражнения

854. Выполните умножение многочленов:

а) (х - у)(х + у);
б) (p + q)(p - q);
в) (р - 5)(р + 5);
г) (х + 3)(х - 3);
д) (2х -1)(2х + 1);

е) (7+ 3у)(3у - 7);
ж) (n - 3m)(3m + n);
з) (2а - 3b(3b + 2а);
и) (8с + 9d)(9d - 8с).

855. Выполните умножение:

а) (у - 4)(y + 4);
б) (р - 7)(7 + р);
в) (4 + 5y)(5y - 4);

г) (7х - 2)(7х + 2);
д) (8b + 5а) (5а - 8b);
е) (10х - 6с) (10х + 6с).

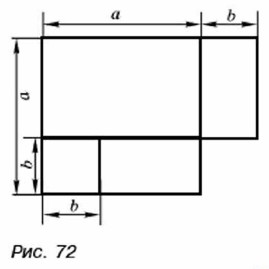
856. С помощью рисунка 72 разъясните геометрический смысл формулы (а - b)(а + b) = а² - b² для положительных а и b, удовлетворяющих условию а > b.

Продолжение >>>