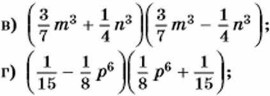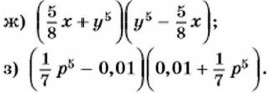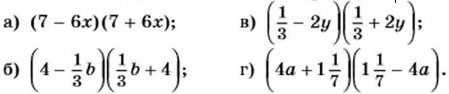Умножение разности двух выражений на их сумму (продолжение)

857. Представьте в виде многочлена произведение:

а) (х² - 5)(х² + 5);

б) (4 + y²)(y² - 4);

в) (9а - b²)(b² + 9а);

г) (0,7х + y²)(0,7х - у²);

д) (10р² - 0,3q²)(10р² + 0,Зq²);

е) (а³ - b²)(а³ + b²);

ж) (с⁴ + d²)(d² - с⁴);

з) (5х² + 2у³) (5х² - 2у³);

и) (1,4с - 0,7р³)(0,7р³ + 1,4с);

к) (1,3а⁵ - 0,1b⁴)(1,3а⁵ + 0,1b⁴).

858. Впишите вместо знака * одночлен так, чтобы получилось тождество:

а) (2а + *)(2а - *) = 4а² - b²;

б) (* - 3х)(* + 3х) =16у² - 9х²;

в) (* - b⁴)(b⁴ + *) = 121а¹⁰ - b⁸;

г) m⁴ - 225с10 = (m² - *)(* + m²).

859. Представьте в виде многочлена:

а) (3х² - 1)(3х² + 1);
б) (5a - b³)(b³ + 5а);

д) (0,4y³ + 5а²)(5а² - 0,4y³);
е) (1,2с² - 7а²) (1,2с² + 7а²);

860. Найдите значение выражения:

а) (100 - 1)(100 + 1);
б) (80 + 3)(80 - 3);
в) 64 • 56;

г) 201 • 199;
д) 74 • 66;
е) 1002 • 998;

ж) 1,05 • 0,95;
з) 60,1 • 59,9.

861. Найдите значение произведения:

а) 52 • 48;
б) 37 • 43;
в) 6,01 • 5,99;

г) 2,03 • 1,97
д) 17,3 • 16,7;
е) 29,8 • 30,2;

ж) 9,7 • 10,3;
з) 50,2 • 49,8;
и) 4,6 • 5,4.

862. Представьте выражение в виде многочлена, используя соответствующую формулу сокращённого умножения:

а) (-р + х)(х + р);
б) (-а + b)(b - а);
в) (-b - с)(b - с);

г) (х + р)(-х - у);
д) (х - у) (у - х);
е) (-a - b)(-a - b).

863. Представьте в виде многочлена:

а) (-3хр + а)(3хр + а);
б) (-1 - 2a²b)(1 - 2а²b);
в) (12а³ - 7х)(-12а³ - 7х);

г) (-10р⁴ + 9)(9 - 10р⁴);
д) (0,2х + 10y)(10y - 0,2х);
е) (1,1р - 0,3)(0,3 + 1,1р).

864. Выполните умножение:

а) (-m² + 8)(m² + 8);
б) (5y - y²)(y² + 5у);

в) (6n² + 1)(-6a² + 1);
г) (-7ab - 0,2)(0,2 - 7ab)

865. Найдите наибольшее значение выражения:

866. Найдите наибольшее или наименьшее значение выражения, если такое значение существует:

а) (5а - 0,2) (0,2 + 5а);
б) (12 - 7у)(7у + 12);

в) (13а - 0,3) (0,3 + 13а);
г) (10 - 9m)(9m + 10).

867. Представьте в виде многочлена:

а) 2(х - 3)(х + 3);
б) у(у + 4)(y - 4);
в) 5х(х + 2)(х - 2);

г) -3а(а + 5)(5 - а);
д) (0,5x - 7)(7 + 0,5х)(-4х);
е) -5y(-3y - 4)(3у - 4).

868. Представьте выражение в виде многочлена:

а) (b + а)(b - а)²;
б) (х + y)²(y - х);

в) (а - 4)(а + 4)²;
г) (3р + 1)2(1 - 3р).

<<< К началу Окончание >>>