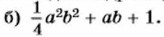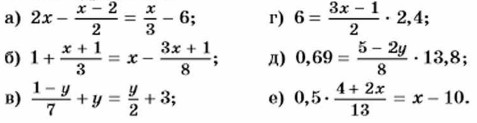|
|
|
|
|
§ 13. Разность квадратов. Сумма и разность кубов Умножение разности двух выражений на их сумму (окончание)869. Выполните умножение:
870. Упростите выражение: а) (0,8x + 15)(0,8x - 15) + 0,36x2; б) 5b2 + (3 - 2b) (3 + 2b); в) 2x2 - (x + 1)(x - 1); г) (3а - 1)(3а + 1)- 17а2; д) 100х2 - (5х-4)(4 + 5х); е) 22с2 + (-3с - 7) (3с - 7). 871. Упростите:
872. Докажите, что квадрат любого целого числа на единицу больше произведения предыдущего и последующего целых чисел. 873. Упростите выражение: а) (x - 2)(x + 2) - x(x + 5); б) m(m - 4) + (3 - m)(3 + m); в) (4x - а)(4x + а) + 2x(x - а); г) 2а(а + b) - (2а + b)(2a - b); д) (5а - 3с)(5а + 3с) - (7с - а)(7с + а); е) (4b + 10с)(10с - 4b) + (-5с + 2b)(5с + 2b); ж) (3x - 4у)2 - (3x - 4р)(3х + 4y); з) (2а + 6b) (6b - 2а) - (2а + 6b)2. 874. (Для работы в парах.) Докажите, что сумма произведения трёх последовательных целых чисел и среднего из них равна кубу среднего числа. 1) Проверьте утверждение на примере чисел 19, 20, 21. 2) Составьте выражение, обозначив через р одно из этих чисел, и выполните преобразование составленного выражения. Одному учащемуся рекомендуем обозначить через р наименьшее из чисел, а другому — среднее из чисел. 3) Проверьте друг у друга правильность преобразований и сравните их сложность. 875. Упростите выражение: а) 5а (а - 8) - 3(а + 2) (а - 2); б) (1 - 4b)(4b + 1) + 6b(b - 2); в) (8р - q)(q + 8p) - (р + q)(p - q); г) (2х - 7у)(2х + 7у) + (2х - 7у)(7у - 2х). 876. Решите уравнение: а) 8m(1 + 2m) - (4m + 3)(4m - 3) = 2m; б) х - 3х(1 - 12х) = 11 - (5 - 6х)(6х + 5). 877. Найдите корень уравнения: а) (6х - 1)(6jc + 1) - 4х(9х + 2) = -1; б) (8 - 9а)а = -40 + (6 - 3а)(6 + 3а). Упражнения для повторения 878. Представьте выражение в виде квадрата двучлена: а) 1 - 4ху + 4х2у2; 879. Докажите тождество: а) (а + b)2 - 4ab = (а - b)2; б) (а - b)2 + 4ab = (а + b)2; в) (х + 3)3 + (х - 3)3 = 2х3 + 54х. 880. Разложите на множители:
881. Решите уравнение:
882. Со станций М и N, расстояние между которыми 380 км, одновременно навстречу друг другу вышли два поезда. Скорость поезда, отправившегося со станции N, была больше скорости другого поезда на 5 км/ч. Через 2 ч после отправления поездам оставалось пройти до встречи 30 км. Найдите скорость поездов.
|
|
|