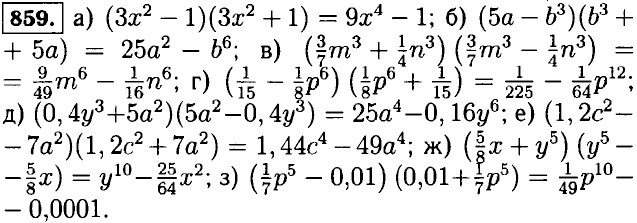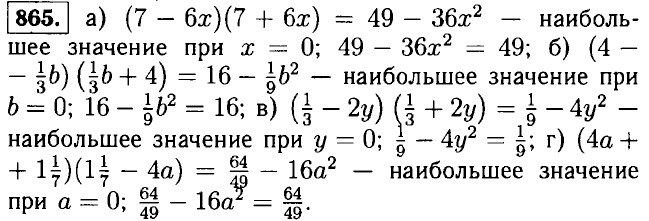Умножение разности двух выражений на их сумму

854. а) (х - у)(х + у) = х² - у²; б) (р + q)(p - q) = p² - q²; в) (р - 5)(р + 5) = р² - 25; г) (х + 3)(х - 3) = х² — 9; д) (2х - 1)(2х + 1) = 4х² - 1; е) (7 + 3у)(3у - 7) - 9у² - 49; ж) (n - 3m)(3m + n) - n² - 9m²; з) (2а - 3b)(3b + 2а) = 4а² - 9b²; и) (8с + 9d)(9d — 8с) = 81d² - 64с².

855. а) (у - 4)(у + 4) = у² - 16; б) (р - 7)(7 + р) = р² - 49; в) (4 + 5у)(5у - 4) = 25у² - 16; г) (7х - 2)(7х + 2) = 49х² - 4; д) (8b + 5а) (5а - 8b) = 25а² - 64b²; е) (10х - 6с)(10х + 6с) = 100х² - 36с².

856. Площадь прямоугольника со сторонами а - b и а + b равна разности площадей квадратов со сторонами а и b.

857. а) (х² - 5)(х² + 5) = х⁴ - 25; б) (4 + у²)(у² - 4) = у⁴ - 16; в) (9а - b²)(b² + 9а) = 81а² - b⁴; г) (0,7х + у²)(0,7х - у²) = 0,49х² - у⁴; д) (10p² - 0,3q²)(10p² + 0,3q²) = 100p⁴ - 0,09q⁴; е) (а³ - b²)(а³ + b²) =а⁶ - b⁴; ж) (с⁴ + d²)(d² - с⁴) = d⁴ - с⁸; з) (5х² + 2у³)(5х² - 2у³) = 25х⁴ - 4у⁶; и) (1,4с - 0,7у³)(0,7у³ + 1,4с) = 1,96с² - 0,49у⁶; к) (1,3а⁵ - 0,1b⁴)(1,3а⁵ + 0,1b4) = 1,69а¹⁰ - 0,01b⁸.

858. a) (2a + b)(2a - b) = 4a² - b²; 6) (4у - 3х)(4у + 3x) = 16y² - 9x²; в) (11a⁵ - b⁴)(b⁴ + 11a⁵) = 121a¹⁰ - b⁸; г) m⁴ - 225c¹⁰ = (m² - 15c⁵)(15c² + m²).

860. a) (100 - 1)(100 + 1) = 100² - 1 = 10000 - 1 = 9999; 6) (80 + 3) (80 - 3) = 80² - 9 = 6400 - 9 = 6391; в) 64 • 56 = (60 - 4) (60 + 4) = 60² - 16 = 3600 - 16 = 3584; г) 201 • 199 = (200 - 1)(200 + 1) = 40000 - 1 = 39999; д) 74 • 66 = (70 - 4) • (70 + 4) = 4900 - 16 = 4884; e) 1002 • 998 = (1000 - 2) (1000 + 2) = 1000000 - 4 = 999996; ж) 1,05 • 0,95 = (1 - 0,05) (1 + 0,05) = 1 - 0,0025 = 0,9975; з) 60,1 - 59,9 = (60 - 0,1)(60 + 0,1) = 3600 - 0,01 = 3599,99.

861. a) 52 • 48 = (50 - 2)(50 + 2) = 2500 - 4 = 2496; 6) 37 • 43 = (40 - 3) • (40 + 3) = 1600 - 9 = 1591; в) 6,01 • 5,99 = (6 - 0,01)(6 + 0,01) = 36 - 0,0001 = 35,9999 г) 2,03 •1,97 = (2 - 0,03)(2 + 0,03) = 4 - 0,0009 = 3,9991; д) 17,3 • 16,7 = (17 - 0,3)(17 + 0,3) = 289 - 0,09 = 288,91; е) 29,8 • 30,2 = (30 - 0,2)(30 + 0,2) = 900 - 0,04 = 899,96; ж) 9,7 • 10,3 = (10 - 0,3)(10 + 0,3) = 100 - 0,09 = 99,91; з) 50,2 • 49,8 = (50 - 0,2) (50 + 0,2) = 2500 - 0,04 = 2499,96; и) 4,6 • 5,4 = (5 - 0,4) (5 + 0,4) = 25 - 0,16 = 24,84.

862. a) (-y + x)(x + y) = (x- y)(x + y) = x² - y²; 6) (-a + b)b - a) = (b - a)² = b² - 2ab + a²; в) (-b - c)(b - c) = -(b + c)(b - c) = -(b² - c²) = c² - b²; г) (х + у)(-х -у) = -(x + у)² = -(х² + 2ху + у²) = = -x² - 2xу - у²; д) (x - у) (у - х) = -(x - у)² = -(x² - 2ху + у²) = -х² + 2xу - у²; е) (-а - b)(-а - b) = (а + b)(а + b) = (а + b) = а² + 2аb + b².

863. а) (-3ху + а)(3ху + а) = а² - 9х²у²; б) (-1 - 2a²b)(1 - 2a²b) = -(1 + 2а²b)(1 - 2a²b) = -(1 - 4а4b²) = 4а⁴b² - 1; в) (12а³ - 7х)(-12а³ - 7х) = -(12а³ - 7х)(12а³ + 7х) = -(144а⁶ - 49х²) = 49x² - 144а6; г) (-10р⁴ +9)(9 - 10р⁴) = (9 - 10р⁴)² = 81- 180р⁴ + 100р⁸; д) (0,2х + 10у)(10у - 0,2х) = 100y² - 0,04x²; е) (1,1у - 0,3)(0,3 + 1,1 у) = 1,21у² - 0,09.

864. а) (-m² + 8)(m² + 8) = 64 - m⁴; б) (5р - у²)(у² + 5у) = 25у² - у⁴; в) (6n² + 1)(-6n² + 1) = 1 - 36n⁴; г) (-7аb - 0,2)(0,2 - 7аb) = (7ab + 0,2)(7аb - 0,2) = 49а²b² - 0,04.

866. а) (5а - 0,2)(0,2 + 5а) = 25а² - 0,04 — наименьшее значение -0,04 при а = 0; б) (12 - 7у)(7у + 12) = 144 - 49у² — наибольшее значение 144 при у = 0; в) (13а - 0,3) = 169a² - 0,09 — наименьшее значение -0,09 при а = 0; г) (10 - 9m)(9m + 10) = 100 - 81m² — наибольшее значение 100 при m = 0.

867. а) 2 • (х - 3)(х + 3) = 2 • (х² - 9) = 2х² - 18; б) у • (у + 4)(у - 4) = у • (у² - 16) = у³ - 16у; в) 5х • (х + 2)(x - 2) = 5x • (x² - 4) = 5x³ - 20x; г) -3а • (а + 5)(5 - а) = -3а • (25 - а²) = 3а³ - 75а, д) (0,5ж - 7)(7 + 0,5x)(-4х) = -4x • (0,25x² - 49) = 196x - x³; е) -5у • (-3у - 4)(3у - 4) = 5у • (3у + 4)(3у - 4) = 5у • (9у² - 16) = 45у³ - 80у.

<<< К началу Решенния (окончание) >>>