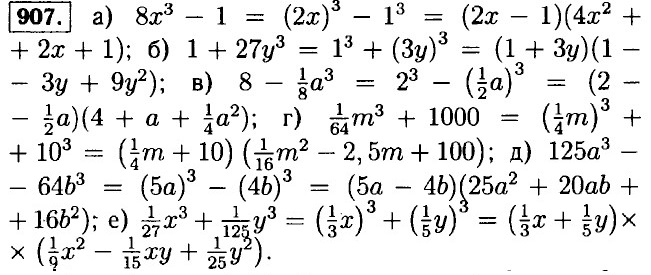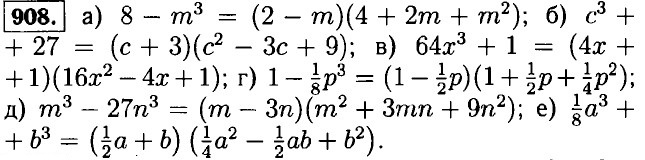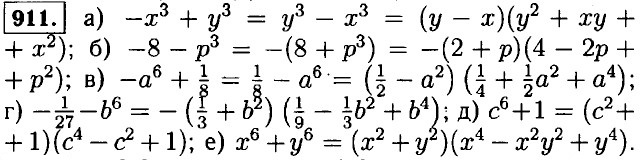Главная >> Домашние работы к учебнику Макарычева. Алгебра 7 класс

Решенния упражнений

Разложение на множители суммы и разности кубов

905. а) х³ + у³ = (х + у)(х² - ху + у²); б) m³ - n³ = (m - n)(m² + mn + n²); в) 8 + а³ = (2 + а)(4 - 2а + а²); г) 27 - у³ = (3-у)(9 + 3у + у²); д) t³ + 1 = (t + 1)(t² - t + 1); е) 1 - с³ = (1 - с)(1 + с + с²).

906. a) c³ - d³ = (с - d)(c² + cd + d²); б) p³ + q³ = (р + q)(р² - pq + q²); в) х³ - 64 = (х - 4)(16 + 4х + х²); г) 125 + а³ = (5 + а)(25 - 5а + а²); д) у³ - 1 = (у - 1 )(у² + у + 1); е) 1 + b³ = (1 + b)(1 - b + b²).

909. a) x³ - у⁶ = (x - y²)(x² + xy² + у⁴); б) a⁶ + b³ = (a² + b)(a⁴ - a²b + b²); в) m⁹ - n³ - (m³ - n)(m⁶ + m³n + n²); г) p³ + k⁹ = (p + k³)(p² - pk³ + k⁶); д) a⁶ + b⁹ = (a² + b³)(a⁴ - a²b³ + 6⁶); e) x⁹ - y⁹ = (x³ - y³)(x⁶ + x³у³ + y⁶).

910. a) c³ + 6⁶ = (c + b²)(c² - cb² + ⁴); 6) a⁹ - b⁶ = (a³ - b2)(a⁶ + a³b² + b⁴); в) x⁶ - 8 = (x² - 2)(x⁴ + 2x² + 4); г) 27 + у⁹ = (3 + y³)(9 - 3y³ + y⁶).

912. a) a³b³ - 1 = (ab - 1)(a²b² + ab + 1); 6) 1 + x³y³ = (1 + xy)(1 - xy + x²y²); в) 8 - a³c³ = (2 - ac)(4 + 2ac + a²c²); г) m³n³ + 27 = (mn + 3)(m²n² - 3mn + 9); д) x³y³ - c³ = (x²y - c)(x⁴y² + x²yc + c²); e) a3 - m³n⁹ = (a - mn³)(a² + amn³ + m²n⁶).

913. а) 327³ + 173³ = (327 + 173)(327² - 327 • 173 + 173²) = 500 • (327² - 327 • 173 + 173²) — делится на 500; б) 731³ - 631³ = (731 - 631)(731² + 731 • 631 + 631²) = 100 • (731² + 731 • 631 + 631²) — делится на 100; в) 211³ + 129³ = (211 + 129)(211² - 211 • 129 + 129²) = 340 • (211² - 211 • 129 + 129²) = 17 • 20 • (211² - 211 • 129 +129²) — кратно 17; г) 356³ • 245³ = (356 - 245)(356² + 356 • 245 + 245²) = 111 • (356² + 356 • 245 + 245²) = 3 • 37 • (356² + 356 • 245 + 245²) — делится на 3.

914. а) 38³ + 37³ = (38 + 37)(38² - 38 • 37 + 37²) = 75х (38² - 38 • 37 + 37²) — делится на 75; б) 99³ - 74³ = (99 - 74)(99² + 99 • 74 + 74²) = 25 • (99² + 99 • 74 + 74²) — делится на 25.

915. а) (11с² + а³)(-а³ + 11с²) = (11с² - а³)( 11с² + а³) = 121с⁴ - а⁶; б) (0,8x + у⁴)(-0,8х - у⁴) = -(0,8x + у⁴)(0,8x + у⁴) = -0,64x² - 1,6xу⁴ - у8; в) (0,3с - 0,2d)(0,2d - 0,3с) = -(0,3с - 0,2d)(0,3с - 0,2d) = -0,09с² + 0,12cd - 0,04d²; г) (6x³ - 4х)(-6x³ - 4х) = (4x - 6х³)(4х + 6x³) = 16x² - 36⁶.

916. а) (x + 2) = х² + 4х + 4 ≠ x⁴ + 4; б) (x - 2)(2 + x) = x² - 4 ≠ 4 - x².

917. а) (2x - 3)² - 2x • (4 + 2x) = 11 ⇒ 4x² - 12x + 9 - 8x - 4x² = 11 ⇒ -20x = 2 ⇒ x = -0,1; б) (4x - 3)(3 + 4x) - 2x • (8x - 1) = 0 ⇒ 16x² - 9 - 16x² + 2x = 0 ⇒ 2x = 9 ⇒ x = 4,5.

<<< К началу