|
|
|
|
|
§ 14. Преобразование целых выражений Преобразование целого выражения в многочлен
Многочлены и, в частности, одночлены являются целыми выражениями. Например, 3,6х2у - 4ху2 + 10x - 0,5у и 10y3 + (3х + у)(х2 - 10у2), 2b(b2 - 10с2) - (b3 + 2с2),
Выражение Выражение 10у3 + (3х + у)(х2 - 10у2) является суммой одночлена 10у3 и произведения многочленов 3х + у и х2 - 10у2. Выражение 2b(b2 - 10с2) - (b3 + 2с2) является разностью между произведением одночлена 2b и многочлена b2 - 10с2 и многочленом b3 + 2с2. Мы знаем, что сумму, разность и произведение многочленов можно преобразовать в многочлен, поэтому каждое из этих целых выражений можно представить в виде многочлена. Выражение
Пример 1. Представим в виде многочлена выражение (х2 + 2)2 - (х - 2)(х + 2)(х2 + 4).
(x4 + 4х2 + 4) - (х2 - 4)(х2 + 4) = х4 + 4х2 + 4 - х4 + 16 = 4х2 + 20. Значит, данное выражение тождественно равно многочлену 4х2 + 20. Преобразование целого выражения в многочлен используется при решении уравнений, доказательстве тождеств, в задачах на делимость и т. п. Пример 2. Докажем, что ни при каком целом n значение выражения (n + 1)(n - 1) - (n - 6)(n + 2) не делится на 4.
(n + 1)(n - 1) - (n - 6)(n + 2) = (n2 - 1) - (n2 - 6n + 2n - 12) = n2 - 1 - n2 + 6n - 2n + 12 = 4n + 11. Мы представили данное выражение в виде суммы 4n + 11. При любом целом я значение первого слагаемого делится на 4; второе слагаемое — число 11 — не делится на 4. Поэтому при любом целом я значение суммы 4n + 11, а значит, и значение исходного выражения (n + 1)(n - 1) - (n - 6)(n + 2) не делится на 4. Упражнения 918. Какие из выражений 2х2у, 4а2 - b(а - 3b), 919. Представьте в виде многочлена: а) сумму многочлена х3 + 7х2 + 8 и произведения многочленов х2 - 6х + 4 и х - 1; б) разность произведения многочленов а2 + 7а - 4 и а -3 и многочлена а3 + 4а2 - 29а +11.
|
|
|



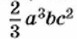 — целые выражения. Примерами целых выражений служат такие выражения:
— целые выражения. Примерами целых выражений служат такие выражения:
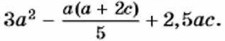
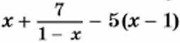 не является целым, так как в нём используется деление на выражение с переменной.
не является целым, так как в нём используется деление на выражение с переменной.
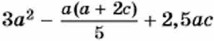 отличается от рассмотренных тем, что в нём содержится деление на число, отличное от нуля. Бели деление заменить умножением на число, обратное делителю, то получится выражение
отличается от рассмотренных тем, что в нём содержится деление на число, отличное от нуля. Бели деление заменить умножением на число, обратное делителю, то получится выражение 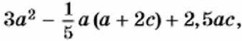 которое, как и предыдущие выражения, составлено из многочленов с помощью действий сложения, вычитания, умножения. Поэтому это целое выражение также можно представить в виде многочлена.
которое, как и предыдущие выражения, составлено из многочленов с помощью действий сложения, вычитания, умножения. Поэтому это целое выражение также можно представить в виде многочлена.
 Имеем
Имеем

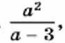
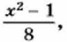
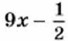 являются целыми?
являются целыми?