|
|
|
|
Главная >> Домашние работы к учебнику Макарычева. Алгебра 7 класс |
|
|
Решенния упражнений Преобразование целого выражения в многочлен918. 2x2у; 4а2 - b • (а - 3b);
919. а) х3 + 7х2 + 8 + (x2 - 6х + 4) (x - 1) = x3 + 7x2 + 8 + x3 - x2 - 6x2 + 6x + 4x - 4 = 2x3 + 10x + 4; б) (а2 + 7а - 4) (а - 3) - (а3 + 4а2 - 29а + 11) = а3 - 3а2 + 7а2 - 21а - 4а + 12 - а3 - 4а2 + 29а - 11 = 4а + 1. 920. a) 4(m - n)2 + 4m • (m - n) = 4 • (m2 - 2mn + n2) + 4m2 - 4mn = 4m2 - 8mn + 4n2 + 4m2 - 4mn = 8m2 - 12mn + 4n2; 6) 5x • (x - y) - 2(y - x)2 = 5x2 - 5xy - 2 • (y2 - 2xy + x2) = 5x2 - 5xy - 2y2 + 4xy - 2x2 = 3x2 - 2y2 - ху, в) (у + 7)2 - 2 • (у + 10)(у + 4) = у2 + 14у + 49 - 2 • (у2 + 4y + 10у + 40) = у2 + 14y + 49 - 2y2 - 28у - 80 = -у2 - 14y - 31; г) (x - 5)(б + 4х) - 3(1 - x)2 = 6x + 4х2 - 30 - 20x - 3 • (1 - 2х + х2) = 4х2 - 14х - 30 - 3 + 6х - 3х2 = х2 - 8х - 33. 921. а) (3m - а)(а + 3m) - (2а + m)(3а - m) = 9m2 - а2 - (ба2 - 2am + 3am - m2) = 9m2 — а2 - ба2 - am + m2 = 10m2 - 7а2 - аm; б) (х - 4у)(х + 3у) + (х - 3у)(3у + х) = х2 + 3ху - 4ху - 12у2 + х2 - 9у2 = 2x2 - ху - 21у2. 922. При а = 2х - 5, b = 8x + 1, с = 4х - 2: ab - с2 = (2x - 5)(8x + 1) - (4х - 2)2 = 1бх2 + 2х - 40х - 5 - (16x2 - 1бх + 4) = 16х2 - 38x - 5 - 1бх2 + 16х - 4 = -22х - 9. 923. (2n + 1)(n + 5) - 2 • (n + 3)(n - 3) - (5n + 13) = 2n2 + 10n + n + 5 - 2 • (n2 - 9) - 5n -13 = (2n2 - 2n2) + (10n + n — 5n) + (5 + 18 - 13) = 6n + 10 = 6 • (n + 1) + 4 — значит данное выражение ни при каком целом n не делится на 6. 924. 1) (n + 8)(n - 4) - (n + 3)(n - 2) = n2 - 4n + 8n - 32 - (n2 - 2n + 3n - б) = (n2 - n2) + (4n - n) + (-32 + б) = 3n - 26. 2) Так как 3n — кратно 3, значит сумма — 26 и пропущенного числа должна делится на 3. 3) Числа -1; 2; 5; 8; 11; 14; 17; 20; 23; 26; 29... удовлетворяют условия задачи. 925. а) х • (х + 2)(х - 2) - х • (х2 - 8) = 16 ⇒ х • (х2 - 4) - х • (х2 - 8) = 16 ⇒ х • (х2 - 4 - х2 + 8) = 16 ⇒ х • 4 = 16 ⇒ х = 4; б) 2у • (4у - 1) - 2(3 - 2у)2 = 48 ⇒ 8у2 - 2у - 2 • (9 - 12у + 4у2) = 48 ⇒ 8у2 - 2у - 18 + 24у - 8у2 = 48 ⇒ 22у = 66 ⇒ у = 3. 926. а) х2 • (х + 2) - х(х + 1)2 = 5х + 9 ⇒ х3 + 2х2 - х • (х2 + 2х + 1) = 5х + 9 ⇒ х3 + 2х2 - х3 - 2х2 - х = 5х + 9 ⇒ 6х = -9 ⇒ х = -1,5; б) (у - 3)2 + 3 • (у + 2) (у - 2) = 9 + 4у2 ⇒ у2 - 6у + 9 + 3у2 - 12 = 9 + 4у2 ⇒ 6у = -12 ⇒ у = -2. 927. а) (а - 1)(а2 + 1)(а + 1) - (а2 - 1)2 - 2• (а2 - 3) = (а2 - 1)(а2 + 1) - (а2 - 1)(а2 - 1) - 2 • (а2 - 3) = (а2 - 1)(а2 + 1 - а2 + 1) - 2 • (а2 - 3) = 2 • (а2 - 1) = 2 • (а2 - 3) = 2 • (а2 - 1 - а2 + 3) = 2 • 2 = 4 — значение выражения не зависит от значения переменной; б) (а2 - 3) - (а -2)(а2 + 4)(а + 2) - 6 • (5 - а2) = а4 - 6а2 + 9 - (а2 - 4)(а2 + 4) - 30 + 6а2 = а4 - 21 - а4 + 16 = -5 — значение выражения не зависит от значения переменной. 928. а) (у - 3)(у2 + 9)(у + 3) - (2у2 - у)2 - 19 = (y2 - 9)(у2 + 9) - (4у4 - 4у3 + у2) - 19 = у4 - 81 - 4у4 + 4y4 - y2 - 19 = -3у4 + 4у3 - у2 - 100; б) (1 - а)(1 - а2) + (1 + а)( 1 + а2) - 2а • (1 + а)(а - 1) = 1 - а2 - а + а3 + (1 + а)(1 + а2 - 2а2 + 2а) = а3 - а2 - а + 1 + 1 - а2 + 2а + а - а3 + 2а2 = 2а + 2. 929. а) (а - 3с)(4с + 2а) + 3с • (а + 3с) = 4ас + 2а2 - 12с2 - бас + 3ас + 9с2 = 2а2 - 3с2 + ас и (2а - с) (3с + 5а) - 8а2 = 6ас + 10а2 - 3с2 - 5ас - 8а2 = 2а2 - 3с2 + ас, значит (а - 3с)(4с + 2а) + 3с • (а + Зс) = (2а - с)(3с + 5а) - 8а2; б) (1 - 2b)(1 - 5b + b2) + (2b - 1)(1 - 6b + b2) = (1 - 2b) (1 — 5b + b2) - (1 - 2b) (1 - 6b + 62) = (1 - 2b)(1 - 5b + b2 - 1 + 6b - b2) = (1 - 2b) • b = b • (1 - 2b)
931. а) -20х4у2 - З5x3у3 = -5х3у2 • (4х + 7у); б) 3а3b2с + 2c3 - 3аb2с • (а2 + 3c2); в) -1,2а3b + 1,2b4 = 1,26 • (b3 - 3) = 1,26 • (b - а)(b2 + аb + а2); г) 7,2x4у4 - 1,8x4у2 = 1,8х4у2 • (4у2 - 1) = 1,8х4у2 • (2у-1)(2у + 1). 932. Пусть велосипедист от деревни до станции ехал t ч, тогда на обратный путь он затратил t + 1 ч. Расстояние от деревни до станции и от станции до деревни одинаковое, значит 15t = 10 • (t + 1) ⇒ 15t = 10t + 10 ⇒ t = 2 ⇒ 15t = 30. Ответ: расстояние от деревни до станции 30 км.
|
|
|



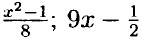 — являются целыми выражениями.
— являются целыми выражениями.
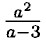 — не является целым, так как в нём используется деление на выражение с переменной.
— не является целым, так как в нём используется деление на выражение с переменной.