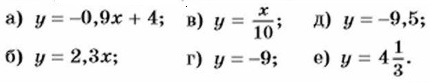Применение различных способов для разложения на множители (окончание)

946. Разложите на множители:

а) х² - у² - х - у;
б) а² - b² - а + b;

в) m + n + m² - n²;
г) k² - k - р² - р.

947. Представьте в виде произведения:

а) а - b + а² - b²; б) с² + d - d² + с.

948. (Для работы в парах.) Используя калькулятор, найдите значение многочлена 3,5х³ - 2,1х² + 1,9дс - 16,7 при х = 3,7.

1) Пусть один из вас вычислит с помощью калькулятора сначала значения каждого члена многочлена, затем значение многочлена, а другой выполнит преобразование многочлена по образцу, предложенному в примере 4 на с. 187, затем сделает вычисления с помощью калькулятора.

2) Отметьте затрату времени на выполнение задания в каждом случае.

3) Сравните полученные результаты и время, затраченное на решение задачи.

949. Решите уравнение:

а) х³ - х = 0;
б) 9х - х³ = 0;

в) х³ + х² = 0;
г) 5х⁴ - 20х² = 0.

950. Решите уравнение:

а) х³ + х = 0; б) х³ - 2х² = 0.

951. Докажите, что значения многочлена х³ - х при целых значениях х кратны числу 6.

952. Докажите, что разность квадратов двух последовательных нечётных чисел делится на 8.

953. Докажите, что если к произведению трёх последовательных целых чисел прибавить среднее из них, то полученная сумма будет равна кубу среднего числа.

Упражнения для повторения

а) (6x - 1)(6х + 1) - (12x - 5)(3x + 1) при x = 0,2;

б) (5 + 2х)² - 2,5x(8x + 7) при jc = -0,5.

955. Не выполняя построения, найдите координаты точек пересечения с осями координат графика функции:

а) у = 0,24x + 6;
б) у = -5х - 1,8;

в) у = -0,6x + 4,2;
г) у = -х - 3,8.

956. Покажите, как примерно расположен в координатной плоскости график функции:

Контрольные вопросы и задания

1. Приведите пример целого выражения и выражения, не являющегося целым.

2. Какие действия надо выполнить и в каком порядке, чтобы представить целое выражение 4х(3 - х)² + (х² - 4)(х + 4) в виде многочлена?

3. Какие способы разложения многочленов на множители вам известны?

<<< К началу Решенния >>>