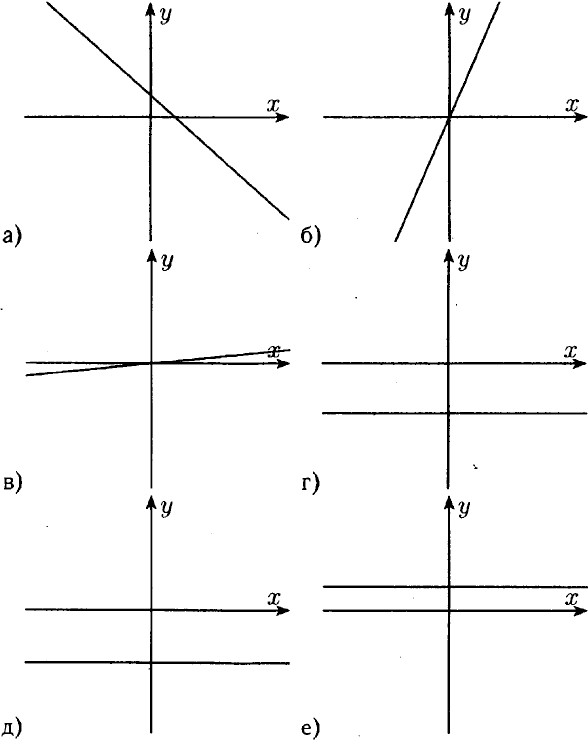
Применение различных способов для разложения на множители (окончание)

948. При х = 3,7 ⇒ 3,5x³ - 2,1x² + 1,9x - 16,7 = 177,2855 - 28,749 + 7,03 - 16,7 = 138,8665 и 3,5x³ - 2,1x² +1,9х - 16,7 = (3,5х² - 2,1х +1,9) • x - 16,7 = ((3,5х - 2,1) • х + 1,9) • х - 16,7 = 138,8665.

949. а) х³ - х = 0 ⇒ х • (х² - 1) = 0 ⇒ х = 0 или х = ±1;

б) 9х - х³ = 0 ⇒ х • (9 - х²) = 0 ⇒ х = 0 или х = ±3;

в) х³ + х² = 0 ⇒ х² • (x + 1) = 0 ⇒ х = 0 или х = -1;

г) 5х⁴ - 20х² = 0 ⇒ 5х² • (х² - 4) = 0 ⇒ x = 0 или х = ±2;

950. а) х³ + х = 0 ⇒ х • (х² + 1) = 0 ⇒ х² + 1 — при-любом значении х больше 0, значит х = 0;-б) х³ - 2х² = 0 ⇒ х² • (х - 2) = 0 ⇒ x = 0 или х = 2;

951. Пусть х³ - х = х • (х² - 1) = x • (x - 1)(x + 1) — три последовательных числа. Из двух последовательных чисел обязательно одно делится на два, а из трёх последовательных чисел обязательно одно делится на 3, значит х³ - х делится на 2 и на 3, а значит х³ - х делится на 6.

952. Пусть 2n + 1, 2n + 3 — два последовательных нечетных числа, разность их квадратов равна (2n + 3)² - (2n + 1)² = 4n² + 12n + 9 - 4n² - 4n - 1 = 8n + 8 = 8 • (n + 1), и она делится на 8.

953. Пусть n, n + 1, n + 2 — три последовательны х целых числа. Их произведение п • (n + 1)(n + 2) = n • (n² + 2n + n + 2) = n³ + 3n² + 2n, а полученная сумма n³ + 3n² + 2n + n + 1 - n³ + 3n² + 3n + 1 = (n + 1)³.

954. а) (6х - 1)(6х + 1) - (12х - 5)(3х + 1) = 36х² -1 - (36х² + 12х - 15х - 5) = 36х² - 36х² + 3х + 5 - 1 = 3х + 4: при х = 0,2 ⇒ 3х + 4 = 0,6 + 4 = 4,6;

б) (5 + 2х)² - 2,5х • (8х + 7) = 25 + 20х + 4х² - 20х² - 17,5х = -16х² + 2,5х + 25: при х = -0,5 ⇒ -16х² + - 2,5х + 25 = -4 - 1,25 + 25 = 19,75.

955. а) у - 0,24х + 6 ⇒ 0,24х = у - 6 ⇒ х 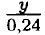= -25. График пересекает ось у при х = 0; у - 6; точка пересечения (0; 6). График пересекает ось х при у = 0; х = 25; точка пересечения (25;0).

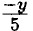б) у = -5х — 1,8 ⇒ 5х = -у - 1,8 4 х = - 0,36. График пересекает ось у при х - 0; у = -1,8; точка пересечения (0; -1,8). График пересекает ось х при у - 0; х = -0,36; точка пересечения (-0,36; 0).

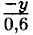в) у = -0,6х + 4,2; 0,6х = -у + 4,2; х = + 7. График пересекает ось у при х = 0; у = 4,2; точка пересечения (0; 4,2). График пересекает ось х при у = 0; х = 7; точка пересечения (7; 0).

г) у = -х - 3,8; х = -у - 3,8. График пересекает ось у при х = 0; у = -3,8; точка пересечения (0; -3,8). График пересекает ось х при у = 0; х = -3,8; точка пересечения (-3,8; 0).

956.

<<< К началу